Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 08. 2010 21:51 — Editoval jelena (12. 04. 2014 23:09)
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Matematická Olympiáda, semináře a další soutěže
Matematická olympiáda: http://math.muni.cz/mo
BRKOS: http://ganymed.math.muni.cz/brkos
PRASE: http://mks.mff.cuni.cz
MaM: http://mam.mff.cuni.cz
Internetová olympiáda VUT Brno pro SŠ
... a spousta dalších rozjíždějí své další ročníky.
Pokud s nimi chcete pomoct, rádi Vám pomůžeme vyřešit návodné úlohy (čti úlohy ze starších ročníků) v sekci Zajímavých úloh ze střední školy.
je to porušení pravidel fóra a je to proti myšlence uvedených soutěží.
Jelena (přidáno 16.02.2013) (zdroj pro diskusi): "Úlohy aktuálního ročníku soutěží považujeme za "starší úlohy" po vystavení oficiálního řešení na stránce pořadatele, nebo následující den po uzávěrce příslušného kola. Domácí a školní kolo Matematické olympiády se považuje za ukončené následující den po termínu okresního kola".
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#2 27. 08. 2010 10:42 — Editoval byk7 (16. 10. 2010 15:40)
Re: Matematická Olympiáda, semináře a další soutěže
Fyzikální olympiáda: http://fo.cuni.cz/
Logická olympiáda: http://www.logickaolympiada.cz/
Olympiáda z programování: http://mo.mff.cuni.cz/p/ (u nás spadá pod MO)
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#3 28. 08. 2010 02:29 — Editoval Spybot (02. 01. 2011 03:51)
#4 29. 08. 2010 15:11 — Editoval pizet (29. 08. 2010 15:12)
Re: Matematická Olympiáda, semináře a další soutěže
o programovaní a algoritmizácií
http://ksp.mff.cuni.cz
Do you follow my way? Or you just see a black stain swimming in the Milky Way ...
KSP je určený pre študentov základných a stredných škôl, ktorí majú záujem naučiť sa niečo z oblasti algoritmov, logických úloh, programovania a informatiky.
Offline
#5 17. 10. 2010 00:44
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Matematická Olympiáda, semináře a další soutěže
odkaz na návodné úlohy k MO ze starších ročníků (děkuji za poskytnutí).
Offline
#6 09. 11. 2010 20:13 — Editoval Kondr (09. 11. 2010 20:15)
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Matematická Olympiáda, semináře a další soutěže
MathRace je letos otevřena nejen pro středoškoláky, ale i pro ostatní týmy (ale středoškoláci mohou vyhrát věcné ceny).
Další zdroj úloh (ne úplně návodných, ale tematicky blízkých) pro Olympioniky: http://kondr.ic.cz/liga -- zatím první kolo, brzy přibudou další :) Soutěž je pouze pro svěřence našeho ústavu.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#7 09. 02. 2011 01:55
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Matematická Olympiáda, semináře a další soutěže
Zajímavá mezinárodní soutěž: http://blog.worldmathsday.com/?page_id=1183
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#8 10. 04. 2011 17:17
Re: Matematická Olympiáda, semináře a další soutěže
Neviem kam to mám dať ale na tejto stránke je veľa dorbých vzorovo vypracovaných príkladov z matematiky a fyziky pre stredné školy:
www.priklady.eu
Do you follow my way? Or you just see a black stain swimming in the Milky Way ...
KSP je určený pre študentov základných a stredných škôl, ktorí majú záujem naučiť sa niečo z oblasti algoritmov, logických úloh, programovania a informatiky.
Offline
#9 01. 07. 2011 01:45
Re: Matematická Olympiáda, semináře a další soutěže
Prehľadný Archív MO - väčšinou s riešeniami: http://www.gljs.sk/mo/
1^6 - 2^6 + 3^6 = 666
Offline
#10 23. 09. 2011 16:10
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Matematická Olympiáda, semináře a další soutěže
Do MathRace 2011 zbývají necelé čtyři týdny -- pokud máte zájem soutěžit, zaregistrujte svůj tým co nejdřív na http://mathrace.jdem.cz.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#11 04. 03. 2012 12:32
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Matematická Olympiáda, semináře a další soutěže
INTERSOB 2012
* Máte smysl pro nesmysly?
* Umíte zna(č)kovat?
* Jste rádi konstantní?
* Máte v sobě jiskru?
* Scrabblit či nescrabblit?
* Stopli jste si jaguára?
* Byli jste už v simulatoriu?
Soutěž pro dvou až čtyřčlenné týmy. Přihlašování končí již 17.3.
http://ganymed.math.muni.cz/intersob/
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#12 27. 04. 2013 20:03
Re: Matematická Olympiáda, semináře a další soutěže
Úlohy domácího kola 63. ročníku Matematické olympiády pro žáky středních škol
Kategorie A
1.
Číslo  je součinem tří (ne nutně různých) prvočísel. Zvětšíme-li každé z nich o 1, zvětší se jejich součin o 963. Určete původní číslo
je součinem tří (ne nutně různých) prvočísel. Zvětšíme-li každé z nich o 1, zvětší se jejich součin o 963. Určete původní číslo  .
.
(Pavel Novotný)
2.
Pro libovolná kladná reálná čísla 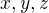 dokažte nerovnost
dokažte nerovnost ,
,
kde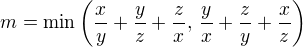 .
.
Zjistěte rovněž, kdy v dokázané nerovnosti nastane rovnost.
(Jaroslav Švrček, Jaromír Šimša)
3.
Označme  střed kružnice vepsané danému trojúhelníku
střed kružnice vepsané danému trojúhelníku 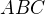 . Předpokládejme, že kolmice na přímku
. Předpokládejme, že kolmice na přímku 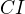 vedená bodem
vedená bodem  protne přímku
protne přímku  v bodě
v bodě  . Dokažte, že kružnice opsaná trojúhelníku
. Dokažte, že kružnice opsaná trojúhelníku 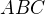 protne úsečku
protne úsečku 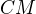 ve vnitřním bodě
ve vnitřním bodě  a že přímky
a že přímky 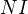 a
a 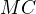 jsou navzájem kolmé.
jsou navzájem kolmé.
(Peter Novotný)
4.
Označme  největšího lichého dělitele čísla
největšího lichého dělitele čísla  . Určete hodnotu součtu
. Určete hodnotu součtu .
.
(Michal „Kenny“ Rolínek)
5.
Kolika různými způsoby můžeme vydláždit plochu 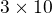 dlaždicemi
dlaždicemi 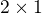 , lze-li je pokládat v obou navzájem kolmých směrech?
, lze-li je pokládat v obou navzájem kolmých směrech?
(Stanislava Sojáková)
6.
V rovině daného trojúhelníku 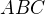 určete všechny body, jejichž obrazy v osových souměrnostech podle přímek
určete všechny body, jejichž obrazy v osových souměrnostech podle přímek 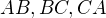 tvoří vrcholy rovnostranného trojúhelníku.
tvoří vrcholy rovnostranného trojúhelníku.
(Pavel Calábek)
Kategorie B
1.
Každému vrcholu pravidelného 63úhelníku přiřadíme jedno z čísel 1, nebo -1. Ke každé jeho straně připíšeme součin čísel v jejích vrcholech a všechna čísla u jednotlivých stran sečteme. Najděte nejmenší možnou nezápornou hodnotu takového součtu.
(Pavel Calábek)
2.
Určete všechny dvojice 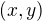 reálných čísel, které vyhovují nerovnici
reálných čísel, které vyhovují nerovnici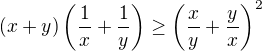 .
.
(Jaroslav Švrček)
3.
Nechť  je libovolný vnitřní bod strany
je libovolný vnitřní bod strany  trojúhelníku
trojúhelníku 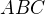 . Na polopřímkách
. Na polopřímkách 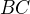 a
a 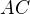 zvolme po řadě body
zvolme po řadě body  a
a  tak, aby platilo
tak, aby platilo  a
a  . Dokažte, že body
. Dokažte, že body 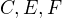 a střed
a střed  kružnice vepsané trojúhelníku
kružnice vepsané trojúhelníku 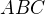 leží na téže kružnici.
leží na téže kružnici.
(Jaroslav Švrček)
4.
Dana napsala na papír trojmístné číslo, které při dělení sedmi dává zbytek 2. Přehozením prvních dvou číslic vzniklo trojmístné číslo, které při dělení sedmi dává zbytek 3. Číslo vzniklé přehozením posledních dvou číslic původního čísla dává při dělení sedmi zbytek 5. Jaký zbytek při dělení sedmi bude mít číslo, které vznikne přehozením první a poslední číslice Danina čísla?
(Pavel Novotný)
5.
V rovině jsou dány body  tak, že úhel
tak, že úhel 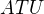 je tupý. Sestrojte trojúhelník
je tupý. Sestrojte trojúhelník 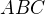 , ve kterém
, ve kterém 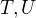 jsou po řadě body dotyku strany
jsou po řadě body dotyku strany 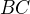 s kružnicí vepsanou a připsanou.
s kružnicí vepsanou a připsanou.
(Šárka Gergelitsová)
6.
Najděte nejmenší reálné číslo  takové, že tyč o délce 1 lze rozlomit na čtyři části délky nejvýše
takové, že tyč o délce 1 lze rozlomit na čtyři části délky nejvýše  tak, aby z žádných tří těchto částí nešlo sestrojit trojúhelník.
tak, aby z žádných tří těchto částí nešlo sestrojit trojúhelník.
(Ján Mazák)
Kategorie C
1.
Určete, jaké nejmenší hodnoty může nabývat výraz  , splňují-li reálná čísla
, splňují-li reálná čísla  dvojici podmínek
dvojici podmínek
(Jaroslav Švrček)
2.
V rovině jsou dány body  neležící na přímce. Sestrojte trojúhelník
neležící na přímce. Sestrojte trojúhelník 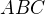 tak, aby
tak, aby  byla pata jeho výšky z vrcholu
byla pata jeho výšky z vrcholu  a
a  bod dotyku strany
bod dotyku strany  s kružnicí vepsanou.
s kružnicí vepsanou.
(Pavel Leischner)
3.
Číslo  je součinem tří různých prvočísel. Zvětšíme-li dvě menší z nich o 1 a největší ponecháme nezměněno, zvětší se jejich součin o
je součinem tří různých prvočísel. Zvětšíme-li dvě menší z nich o 1 a největší ponecháme nezměněno, zvětší se jejich součin o 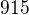 . Určete číslo
. Určete číslo  .
.
(Pavel Novotný)
4.
Ve čtverci 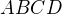 označme
označme  střed strany
střed strany  a
a  střed strany
střed strany 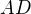 . Úsečky
. Úsečky 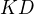 a
a 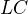 se protínají v bodě
se protínají v bodě  a rozdělují čtverec na dva trojúhelníky a dva čtyřúhelníky. Vypočtěte jejich obsahy, jestliže úsečka
a rozdělují čtverec na dva trojúhelníky a dva čtyřúhelníky. Vypočtěte jejich obsahy, jestliže úsečka  má délku 1 cm.
má délku 1 cm.
(Leo Boček)
5.
Dokažte, že pro každé liché přirozené číslo  je součet
je součet  dělitelný číslem 96.
dělitelný číslem 96.
(Jaromír Šimša)
6.
Šachového turnaje se zúčastnilo 8 hráčů a každý s každým odehrál jednu partii. Za vítězství získal hráč 1 bod, za remízu půl bodu, za prohru žádný bod. Na konci turnaje měli všichni účastníci různé počty bodů. Hráč, který skončil na 2. místě, získal stejný počet bodů, jako poslední čtyři dohromady. Určete výsledek partie mezi 4. a 6. hráčem v celkovém pořadí.
(Vojtěch Bálint)
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#13 12. 04. 2014 21:41
- julinka-bublinka
- Zelenáč
- Příspěvky: 1
- Reputace: 0
Re: Matematická Olympiáda, semináře a další soutěže
Úhlopříčky daného čtyřúhelníku jsou osami jeho vnitřních úhlů. Urči jeho obsah, jestliže jedna strana a jedna z jeho úhlopříček mají shodně délku 2 cm.
Toť zadání. Jediné, co mě napadlo bylo, že by se jednalo o deltoid, pak by se ale dvě strany rovnaly délce úhlopříčky. Není sice psáno, že to má být právě jedna strana, ale i tak. Nevím, jestli to má i jinou možnost, proto se tady ptám...
Offline
#14 12. 04. 2014 23:07
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Matematická Olympiáda, semináře a další soutěže
↑ julinka-bublinka:
Zdravím a děkuji za připomenutí další olympiády - přidám kolegovi Kondrovi do úvodního příspěvku. Téma je spíš pro upozornění na olympiády a také na pravidlo ohledně olympiád. Pro Tebe bude přehlednější si založit vlastní téma (a také je to dle pravidel) v sekci "Zajímavých úloh pro SŠ" (jinak v odkazu najdeš řešení této úlohy v roce 2008)
Offline
#15 13. 03. 2015 11:33
- Radovan00000605

- Zelenáč
- Příspěvky: 14
- Reputace: -1
Re: Matematická Olympiáda, semináře a další soutěže
Ahojte. Prosím vas nepomohli by ste mi s ulohou: Nájdite 2015 po sebe iducich zlozenych cisel.
Dakujem.
Offline
#16 13. 03. 2015 13:11
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Matematická Olympiáda, semináře a další soutěže
↑ Radovan00000605:
Zdravím, jednu odpověď již máš tady, opět jsi ale OT, založ si, prosím, vlastní téma. Děkuji.
Offline
#17 25. 03. 2015 15:05
- Radovan00000605

- Zelenáč
- Příspěvky: 14
- Reputace: -1
Re: Matematická Olympiáda, semináře a další soutěže
Dobrý deň, chcela by som sa opýtaž na príklad: Šachového turnaja sa zúčastnilo 10 krát viac chlapcov ako dievčat.
Chlapci však získali len 4,5 krát viac bodov ako dievčatá. V turnaji
hral každý s každým práve raz. Za víťazstvo sa získaval 1 bod, za
remízu 0,5 bodu a za prehru 0 bodov. Kto vyhral turnaj?
označim si počet dievčat x a počet chlapcov 10x ,dalej počet bodov dievcat y a počet bodov chlapcov 4,5y...pomože mi to? ci by som sa mala uberat nejako inak? nepomohli by ste mi prosim? dakujem :)
Offline
#18 25. 03. 2015 15:50
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Matematická Olympiáda, semináře a další soutěže
↑ Radovan00000605:
Zdravím, pokud chceš prodiskutovat úlohu starší olympiády, nebo jinou starší soutěžní úlohu, potom si založ téma v sekci Zajímavých např. pro SŠ, nebo si zvol jinou vhodnou sekci pro vlastní téma viz ↑ můj předchozí příspěvek:. Děkuji.
Offline
#19 08. 10. 2016 16:59
- petrik_ch

- Místo: Topoľčany
- Příspěvky: 241
- Škola: ZS Tribecska Topolcany
- Pozice: priatel skoly, absolvent, rodic
- Reputace: 2
- Web
Re: Matematická Olympiáda, semináře a další soutěže
Nejake materialy k MO a FO z min. rocniku jsou i tady:
https://www.hackmath.net/cz/priklady/ma … -olympiada
Offline
#20 16. 10. 2016 13:50
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Matematická Olympiáda, semináře a další soutěže
↑ petrik_ch:
Zdravím a děkuji za odkaz,
ale opět řeknu, že za Tvoji stránkou je určitě hodně práce, bohužel se vyskytuji chyby (příklad), ale to se dá popř. opravit. Horší je, že při řešení zcela vynecháváš rozbor úloh (což je u olympiád hodně podstatné), chybí popis zavedených proměnných, postup řešení není přiměřený třídě, pro kterou je úloha zadaná, nebo postup zcela chybí (2+2=4 asi není postup) apod. Určitě rozbor řešení dostatečně pokrývají materiály samotné MO a dalších organizátorů, popř. snad jen ponechat zadání, odkaz na oficiální stránku a možnost diskuse v komentářích. Jinak to na kvalitě spíš ubírá, než přidává. Přeji zdar.
Offline
#21 09. 03. 2018 21:39
Re: Matematická Olympiáda, semináře a další soutěže
Dobrý den,
na internetu jsem narazila na konstrukční úlohu a nejsem schopna ji vyřešit (pokud to jde) :Sestrojte pravoúhlý trojúhelník znáte-li jeho obvod a výšku v.
Děkuji za odpovědi
Offline
#22 10. 03. 2018 10:30
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Matematická Olympiáda, semináře a další soutěže
↑ Janca237:
Zdravím, technika bude shodná (úhel máš zadaný sdělením, že trojúhelník je pravoúhlý) Odkaz, podrobnější vysvětlení je v tématu (těchto konstrukcí je na fóru více, úloha je např. v Petákové - viz odkazy.
Je lepší si založit vlastní téma, nevkládat do cizích témat, děkuji.
Offline
#23 08. 07. 2020 16:22
- Anonymjsemjá

- Zelenáč
- Příspěvky: 5
- Reputace: 0
Re: Matematická Olympiáda, semináře a další soutěže
Ahoj, jak se prosím nazývá a zachází s tímto zápisem, který je na letošním zadání MO, kat. B. Mám na mysli  = 35 způsobů.
= 35 způsobů.
Díky moc
Offline
#24 08. 07. 2020 17:41
Re: Matematická Olympiáda, semináře a další soutěže
↑ Anonymjsemjá:Ten zapis sa podoba dvom bezne pouzivanym - jeden je zlomok  , druhy je kombinacne cislo
, druhy je kombinacne cislo 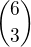 . Lenze
. Lenze 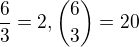 .
.
Offline
#25 08. 07. 2020 20:00
- misaH
- Příspěvky: 13459
Re: Matematická Olympiáda, semináře a další soutěže
↑ Anonymjsemjá:
Nič také neviem nikde nájsť - ktoré kolo?
Offline
