Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 13. 07. 2020 15:52 Příspěvek uživatele misaH byl skryt uživatelem misaH.
#4 13. 07. 2020 18:07
Re: Rovnice kontinuity
↑ Marcia24:
jen doplním ↑ MichalAld:
rozměrovou analýzou snadno zjistíš rozměr té konstanty (při standartní použití symbolů)  , tj. časová změna hmotnosti.
, tj. časová změna hmotnosti.
ale jak už napsal přede mnou, bez dalších podrobností víc nevyčarujeme.
jen nápad:  je povrch nějaké koule a
je povrch nějaké koule a  je hmotnost procházející jednotkovou plochou za jednotku času. Celé se to rovná časovému úbytku hmotnosti.
je hmotnost procházející jednotkovou plochou za jednotku času. Celé se to rovná časovému úbytku hmotnosti.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline


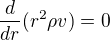 plyne jen to, že
plyne jen to, že 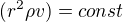 , že ta konstanta je zrovna
, že ta konstanta je zrovna  (ať už to znamená co chce) musí plynout odjinud. Přesněji řečeno, ten fyzikální význam M musí plynout odjinud.
(ať už to znamená co chce) musí plynout odjinud. Přesněji řečeno, ten fyzikální význam M musí plynout odjinud.