Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 06. 2020 07:44
Fermatova Velká Věta
Ahoj všichni,
Fermatova Velká Věta:
Neexistují celá kladná čísla  a
a  , kde
, kde  , pro která
, pro která 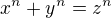 .
.
Nápad k vyřešení:
Za předpokladu, že z> y> x jsou strany trojúhelníku ABC s příslušnými úhly A> B> C, pak můžeme napsat 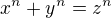 a
a  ze kterého konečně získáme
ze kterého konečně získáme 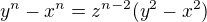 .Jsou diskutovány případy
.Jsou diskutovány případy 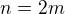 a
a 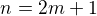 a tak je ukázáno, že rovnice
a tak je ukázáno, že rovnice 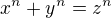 nemá řešení....
nemá řešení....
Je snadno ukázáno , že  kde
kde  .
.
Vše nejlepší,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#2 29. 06. 2020 12:09 — Editoval Ferdish (29. 06. 2020 12:10)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Fermatova Velká Věta
Nič v zlom, ale dokázať Veľkú Fermatovu vetu trvalo storočia, s využitím mohutného matematického aparátu. Ak by tú vetu šlo dokázať tak jednoducho ako to popisuješ, už by to dávno niekto urobil a publikoval, nemyslíš?
Offline
#3 29. 06. 2020 16:59
Re: Fermatova Velká Věta
Ferdish napsal(a):
Nič v zlom, ale dokázať Veľkú Fermatovu vetu trvalo storočia, s využitím mohutného matematického aparátu. Ak by tú vetu šlo dokázať tak jednoducho ako to popisuješ, už by to dávno niekto urobil a publikoval, nemyslíš?
Ahoj,
Ano! Jako Columbusovo vejce!
Řešení Fermatovy velké věty musí být provedeno s koncepty matematiky existující v době Fermata ... a ne jako anglický matematik Andrew Wiles ...
Kde najdu řešení dané matematikem Andrew Wiles?Děkuji mnohokrát!
Vše nejlepší,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#7 30. 06. 2020 05:54
Re: Fermatova Velká Věta
vlado_bb napsal(a):
↑ Dacu: Wiles, Andrew (1995). "Modular elliptic curves and Fermat's Last Theorem". Annals of Mathematics. 141 (3): 443–551.
Ahoj,
Kde najdu pouze demonstrac Fermatově Velké Větě, kterou dal Wiles?Děkuji mnohokrát!
Vše nejlepší,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#9 30. 06. 2020 13:32
Re: Fermatova Velká Věta
↑ vlado_bb:
Kolik skvělých matematiků analyzovalo Wilesův důkaz a kolik z nich ten důkaz pochopilo ???
Vše nejlepší,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#10 30. 06. 2020 13:55
Re: Fermatova Velká Věta
Ahoj všichni,
Z  a
a 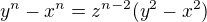 se získá
se získá 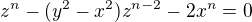 a podle Vièteho vztahů můžeme napsat, že
a podle Vièteho vztahů můžeme napsat, že  což je v rozporu s řádovým vztahem z> y> x> 0.
což je v rozporu s řádovým vztahem z> y> x> 0.
Jaký je závěr?Děkuji mnohokrát
Vše nejlepší,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#11 03. 07. 2020 14:46
- check_drummer

- Příspěvky: 4939
- Reputace: 106
Re: Fermatova Velká Věta
Ahoj, z čeho toto plyne?
Dacu napsal(a):
"Máte úhel beta." "No to nemám."
Offline
#12 03. 07. 2020 14:47
- check_drummer

- Příspěvky: 4939
- Reputace: 106
Re: Fermatova Velká Věta
↑ Ferdish:
Ahoj, já bych neřekl, že je to důkaz, že uvedený postup není důkazem. Opravdu se mohlo stát, že by nikdo nějaký jednouchý postup nenašel. I když je to málo pravděpodobné, tak se v historii vyskytují případy, kdy nějaké problémy byly po delší době vyřešeny nějakým elegantním postupem.
"Máte úhel beta." "No to nemám."
Offline
#13 03. 07. 2020 17:34 — Editoval vanok (03. 07. 2020 17:35)
Re: Fermatova Velká Věta
Pozdravujem ↑ check_drummer:,
Ten vyraz vyuziva ortogonalnu projekciu bodu A na stranu BC.....
Ale potom .....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 20. 07. 2020 06:46 — Editoval Dacu (20. 07. 2020 07:21)
Re: Fermatova Velká Věta
Hello all,
Fermat's Great Theorem:
There are no positive integers  and
and  , where
, where  , for which
, for which 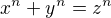 .
.
Demonstration:
It is easily show that  must be the sides of a triangle.
must be the sides of a triangle.
Assuming that  are sides of triangle ABC with corresponding angles
are sides of triangle ABC with corresponding angles  , then we can write
, then we can write 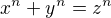 and
and  from which we finally obtain
from which we finally obtain 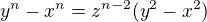 .
.
It is easily show that  where
where  .
.
1) From  and
and 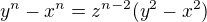 results
results 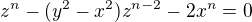 which means that
which means that 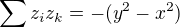 and
and 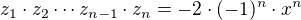 .
.
2) From  and
and 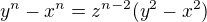 results
results 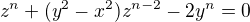 which means that
which means that 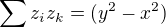 and
and 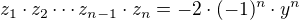
3) From 1) and 2) it results that  , fact impossible because by hypothesis
, fact impossible because by hypothesis  .
.
Quod erat demonstrandum.
Is there anyone who can find a mistake in this demonstration made with elements of mathematics from the time of Fermat?I'm waiting for replies!Thank you very much!
All the best,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#15 21. 07. 2020 00:20 — Editoval vanok (21. 07. 2020 00:34)
Re: Fermatova Velká Věta
Hi Dacu,
Remark 1.
I don’t understand your demonstration in lines 5 to 7 #14.
Remark 2.
For n=4, in # 14, line 8, give  , so
, so 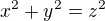 .
.
Which is a contradiction to your line 9
Remark 3.
A useful reading :
https://en.wikipedia.org/wiki/Fermat%27s_Last_Theorem
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#16 21. 07. 2020 06:40 — Editoval Dacu (21. 07. 2020 06:45)
Re: Fermatova Velká Věta
Hello,
vanok napsal(a):
Remark 1.
I don’t understand your demonstration in lines 5 to 7 #14.
What exactly did you not understand from lines 5 to 7 # 14?
vanok napsal(a):
Remark 2.
For n=4, in # 14, line 8, give, so
.
Which is a contradiction to your line 9
For  it results
it results 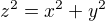 and which together with
and which together with  gives the fact that
gives the fact that  or
or  which contradicts
which contradicts  .
.
vanok napsal(a):
Remark 3.
A useful reading :
https://en.wikipedia.org/wiki/Fermat%27s_Last_Theorem
The demonstration given by Andrew Wiles does not conform to the elements of mathematics known in the time of Fermat ...Did you understand Andrew Wiles' demonstration?How many mathematicians understood Andrew Wiles' demonstration? Thank you very much!
All the best,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#17 21. 07. 2020 08:16
Re: Fermatova Velká Věta
Hi,
What does the word demonstration mean to you?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#18 22. 07. 2020 06:51 — Editoval Dacu (22. 07. 2020 06:52)
Re: Fermatova Velká Věta
vanok napsal(a):
Hi,
What does the word demonstration mean to you?
Hello,
In this case the demonstration is a series of calculations, reasoning, etc. by which the truth of a theorem or the content of a formula is proved.
------------------------------------------------
To obtain the relation 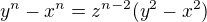 we also used and Law of cosines.
we also used and Law of cosines.
I repeat , "What exactly did you not understand from lines 5 to 7 # 14"?Thank you very much!
All the best,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#19 22. 07. 2020 08:10
Re: Fermatova Velká Věta
Let me summarize: Complete all your statements with demonstrations .
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#20 22. 07. 2020 20:15
- check_drummer

- Příspěvky: 4939
- Reputace: 106
Re: Fermatova Velká Věta
↑ Dacu:
Hi, how do you obtain 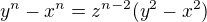 ? It is not enough to say that it follows from the law of cosines.
? It is not enough to say that it follows from the law of cosines.
"Máte úhel beta." "No to nemám."
Offline
#21 23. 07. 2020 18:04 — Editoval Dacu (23. 07. 2020 18:55)
Re: Fermatova Velká Věta
vanok napsal(a):
Let me summarize: Complete all your statements with demonstrations .
Hello,
I will present the respective relationships step by step ....
1) 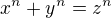
2) 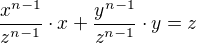
3) 
4) 
5) 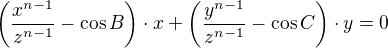
6) 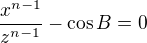 and
and 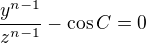
7)  and
and 
8) 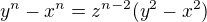
Is my reasoning correct?Thank you very much!
All the best,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#22 23. 07. 2020 21:50 — Editoval check_drummer (23. 07. 2020 22:13)
- check_drummer

- Příspěvky: 4939
- Reputace: 106
Re: Fermatova Velká Věta
↑ Dacu:
Why does 6) follow from 5)? It is not generally true that if ax+by=0, then a=0 and b=0.
From what follows 8)? (Edit: I see it, so it remains to clarify the line above.)
"Máte úhel beta." "No to nemám."
Offline
#23 24. 07. 2020 06:35 — Editoval Dacu (24. 07. 2020 06:36)
Re: Fermatova Velká Věta
check_drummer napsal(a):
↑ Dacu:
Why does 6) follow from 5)? It is not generally true that if ax+by=0, then a=0 and b=0.
From what follows 8)? (Edit: I see it, so it remains to clarify the line above.)
Hello,
From 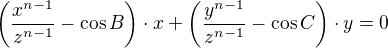 the following possibilities result:
the following possibilities result:
1) 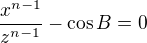 and
and 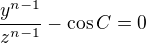 .
.
2) 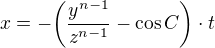 and
and 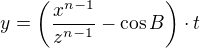 where
where  with
with 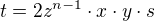 where
where  and
and  .
.
Which of the two possibilities can exist, 1) or 2)?Thank you very much!
All the best,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#24 24. 07. 2020 17:47 — Editoval check_drummer (24. 07. 2020 17:50)
- check_drummer

- Příspěvky: 4939
- Reputace: 106
Re: Fermatova Velká Věta
↑ Dacu:
In 2): Why  should be whole number, ie why it is
should be whole number, ie why it is 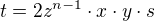 and why
and why  should be whole number?
should be whole number?
"Máte úhel beta." "No to nemám."
Offline
#25 25. 07. 2020 05:52 — Editoval Dacu (25. 07. 2020 06:54)
Re: Fermatova Velká Věta
check_drummer napsal(a):
↑ Dacu:
In 2): Whyshould be whole number, ie why it is
and why
should be whole number?
Hello,
Because  and
and  must be natural numbers greater than zero ....
must be natural numbers greater than zero ....
All the best,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline