Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 03. 08. 2020 09:02
Re: Větička z algebry
podľa pána Bezouta existujú celé čísla 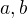 také, že
také, že 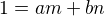 potom
potom 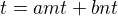 podľa predpokladu existujú celé čísla
podľa predpokladu existujú celé čísla  také, že
také, že 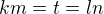 teda
teda 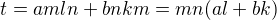
MATH IS THE BEST!!!
Offline
#4 03. 08. 2020 09:57 — Editoval nejsem_tonda (03. 08. 2020 11:27)
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Větička z algebry
Jarrro ti napsal pekny dukaz. Ja zkusim jeste dodat pohled, jak "proste citit, ze to tak je".
Predstavim si cisla t, m, n rozlozena na prvocisla. Prvocisla, ktera jsou obsazena v m nazveme modra. Prvocisla, ktera jsou obsazena v n nazveme cervena. Nesoudelnost rika, ze zadne prvocislo neni zaroven modre i cervene.
Protoze m | t, tak t obsahuje vsechna modra prvocisla v dostatecne velke mocnine. Podobne z delitelnosti n | t plyne, ze t obsahuje i vsechna cervena prvocisla v dostatecne mocnine. Znovu pripomenu, ze mnoziny modrych a cervenych prvocisel se navzajem neprotinaji, takze t je delitelne i soucinem mn (tj. modrymi a cervenymi prvocisly v tech mocninach, ve kterych se objevuji v m, resp. v n)
--------------------------------------------------------------------------------------
Pro jistotu to jeste ukazu na prikladu. Predstavuju si to nejak takhle:

Protoze m | t, tak t obsahuje prvocisla 3, 7, 11 v dostatecnych mocninach, tj. 3 v mocnine aspon 2, 7 v mocnine aspon 5, 11 aspon v mocnine 1. Protoze n | t, tak t obsahuje i prvocisla 5, 13, 19, 61, opet v dostatecnych mocninach.
Takze napriklad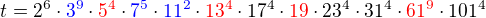
a je proste videt, ze t je "dostatecne modre" i "dostatecne cervene", aby bylo delitelne soucinem mn.
--------------------------------------------------------------------------------------
Da se to napsat cele i tak, aby to byl formalne korektni dukaz, ale bylo by tam hodne indexu a mocnin :) A hlavne - nedavalo by to ten vhled, kvuli kteremu svuj komentar pisu.
Offline
#5 03. 08. 2020 18:33
- check_drummer

- Příspěvky: 4637
- Reputace: 99
Re: Větička z algebry
Ahoj,
co to zkusit úplně přímočaře:
t=m.x, t=n.y, tj. (1) mx=ny, tj. n | x, m | y, tj. x=nu, y=mv a po dosazení do (1) t=mnu=mnv, tj. mn | t.
"Máte úhel beta." "No to nemám."
Offline
#6 03. 08. 2020 19:33
Re: Větička z algebry
Ahoj ↑ check_drummer:,
To mas pravdu, ze sa to da dokazat velmi jednoducho.
Mozno, pre zaciatocnika je najprirozdzenejsie pouzit zakladnu vetu atitmetiky:
Cize to, ze kazde nenulove cislo a rozne od  sa pise, az na usporiadanie, jednoznacne ako sucin striktne kladnych mocnin prvocisiel.
sa pise, az na usporiadanie, jednoznacne ako sucin striktne kladnych mocnin prvocisiel.
Tak znama veta z #2, sa potom jednoducho ukaze vdaka tomu, ze nesudelitelne  a
a  maju v ich rozkladoch len rozlicne prvocisla.
maju v ich rozkladoch len rozlicne prvocisla.
Zvysok tohto dokazu necham citatelom.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 04. 08. 2020 09:45
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Větička z algebry
mx=ny, tj. n | x
Tady skryte vyuzijes te nesoudelitelnosti. Myslim si, ze kdybys tuto implikaci chtel zduvodnit podrobne, nevyhnes se tomu, co jsem ukazoval s modrymi a cervenymi prvocisly (coz je totez o cem pise i vanok).
Offline
#9 05. 08. 2020 20:47
- check_drummer

- Příspěvky: 4637
- Reputace: 99
Re: Větička z algebry
↑ nejsem_tonda:
Ahoj, využívám tvrzení, že pokud nsd(m,n)=1, tak potom z n | mx plyne, že n | x. Zkusím se zamyslet, zda to půjde dokázat bez nutnosti elemntárního rozkladu...
"Máte úhel beta." "No to nemám."
Offline
#10 05. 08. 2020 22:14 — Editoval vanok (05. 08. 2020 22:15)
Re: Větička z algebry
Ahoj ↑ check_drummer:,
Mozes pouzit kontrapoziciu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

 značí největší společný dělitel čisel n,n
značí největší společný dělitel čisel n,n myslíme nejmenší exponent k takový, že
myslíme nejmenší exponent k takový, že