Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Lineárna algebra, podmnožiny a podpriestory (TOTO TÉMA JE VYŘEŠENÉ)
#1 21. 10. 2020 08:58
Lineárna algebra, podmnožiny a podpriestory
Nemôžem pochopiť ako treba zistiť, či tvorí podmnožina nejaký podpriestor. Budem veľmi šťastný ak mi niekto pomôže. Dakujem.
Zadanie: Rozhodnite, či podmnožina
a) W= {[x, y, z]T | 3x+z= 0, x+ 2y = 2} v priestore R^3 tvori podpriestor R^3
b) L= {[x1, x2, x3...]Т | xj=0 pre j Є {2, 4,6,...]} v priestore R∞ tvorí podpriestor R∞ ;
e) K = 0 a 0 |
b 0 c | ad-bc=0
0 d 0 |
V priestore M3×3(R) tvorí podpriestor M3×3(R). Svoje rozhodnutie zdôvodnite.
Offline
- (téma jako vyřešené označil(a) Kart)
#2 21. 10. 2020 10:26
Re: Lineárna algebra, podmnožiny a podpriestory
↑ Kart:Kedy je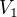 
podpriestorom 
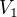? Urcite najdes v texte, ktory pouzivas, nutnu a postacujucu podmienku tykajucu sa linearnych kombinacii prvkov . Nasiel si? V tom pripade mame cast b hotovu systemom "pozriem a vidim", ano?
Offline
#3 21. 10. 2020 11:04
Re: Lineárna algebra, podmnožiny a podpriestory
↑ vlado_bb: nevidím toto. Tá podmienka je, že keď násobím skalárom tieto vektory alebo sčitavame ich, tak ony zostanú v tom istom podpriestore? Mám problémy s touto témou
Offline
?#5 21. 10. 2020 11:18
Re: Lineárna algebra, podmnožiny a podpriestory
↑ vlado_bb: myslím si, že b je správne,pretože tu platí táto podmienka. Áno?
Offline
#7 21. 10. 2020 12:27
Re: Lineárna algebra, podmnožiny a podpriestory
↑ vlado_bb: čo potrebujem napísať v časti c? Že zložky matice a,b,c,d môžu byť všetky nuly či napr. a=0 aj b=0 alebo a=0 aj b=0. Ale to nám nevadí a nákončí táto matica vždy tvori podpriestor R^3? A v a), kde z je voľná premenná to bude tiež správne?
Offline
je 
, podobne ako si to robil v casti b.#9 21. 10. 2020 12:42
Re: Lineárna algebra, podmnožiny a podpriestory
↑ vlado_bb: overil som to, a pochopil som, že existujú takéto matice, ale nie všetky. Tak to znamená, že časť c je nesprávna. A časť a je správna, áno?
Offline
#11 21. 10. 2020 12:49
#13 21. 10. 2020 12:58
Re: Lineárna algebra, podmnožiny a podpriestory
↑ vlado_bb: Teraz označím, posledná otázočka, tak a je nesprávne, kvôli tomu, že tam nesedí ten nulový vektor?
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Lineárna algebra, podmnožiny a podpriestory (TOTO TÉMA JE VYŘEŠENÉ)