Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Rozvoj realne funkcie na mocninovy rad
#1 13. 11. 2020 10:47 — Editoval vanok (13. 11. 2020 12:21)
Rozvoj realne funkcie na mocninovy rad
Pozdravujem,
Tu dame do popredia prakticke metody, ktore je uzitocne vediet.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 14. 11. 2020 04:04 — Editoval vanok (14. 11. 2020 18:57)
Re: Rozvoj realne funkcie na mocninovy rad
Nech je dana funkcia f realnej premennej, o ktorej chceme vediet ci existuje mocninovy rad 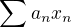 ktoreho polomer konvergencie je R (= nenulove realne cislo) a
ktoreho polomer konvergencie je R (= nenulove realne cislo) a ![kopírovat do textarea $\forall x \in ]-R;R[, f(x)=\sum_{n=0}^{+\infty}a_nx^n$](/mathtex/df/dff8693c23f68a3cfe03d7e38ba91db9.gif)
Poznamka: tu ide o rad centrovany v pociatku 0 (a na tuto situaciu, sa mozme vzdy dostat, lebo povieme, ze funkcia f je rovzvinutelne na mocninovy rad v otvorenom intervale stredu v bode a, ak funkcia  je rozvinutelna na mocninovy rad v bode 0$ ).
je rozvinutelna na mocninovy rad v bode 0$ ).
Tiez, tu bude rozlisovany tento pojem s limitivanym rozvojom funkcie f.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 14. 11. 2020 13:22
Re: Rozvoj realne funkcie na mocninovy rad
Ahoj ↑ MichalAld:,
Pouzivam, oznacenia ako tu .
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 04. 12. 2020 22:44 — Editoval vanok (04. 12. 2020 22:49)
Re: Rozvoj realne funkcie na mocninovy rad
Teraz tu popisem bezne pouzivane metody, tykajuce sa specialnych situacii.
1) pripad, ked mame somacny vzorec.
To je pripad aj geometrickeho radu.
Vieme , ze pre [mathjax]x[/mathjax] take, ze [mathjax]x\ne 1[/mathjax] mame tento vzorec :
[mathjax]1+x +x^2+ ... +x^n=\frac {1-x^{n+1}}{1-x}[/mathjax]
Tak ak [mathjax]x[/mathjax] je take, ze [mathjax]|x| \lt 1[/mathjax] rad [mathjax]\sum_{n\ge 0}^{}x^n[/mathjax] konverguje k [mathjax]\frac 1{1-x} [/mathjax].
A pre [mathjax]x[/mathjax] take, ze [mathjax]|x|> 1[/mathjax] rad diverguje ( co tiez dokazuje, rad [mathjax]\sum_{n\ge 0}^{}x^n[/mathjax] ma polomer konvergencie R=1)
Co piseme [mathjax] \frac 1{1-x}= 1+x +x^2+ ... +x^n+... R=1[/mathjax]
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 04. 12. 2020 23:47 — Editoval vanok (04. 12. 2020 23:48)
Re: Rozvoj realne funkcie na mocninovy rad
↑ MichalAld:,
Ano. Tu budem davat priklady na tie najzaujimavejsie situacie.
Co sa tyka #5, skutocne je to tak... vsak tam ide o geometricky rad.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 05. 12. 2020 11:36
Re: Rozvoj realne funkcie na mocninovy rad
Pozdravujem ↑ MichalAld:,
Tu v pripade 2) dam priklady rozvojov realnych funkcii na mocninove rady, ktore daju nast vdaka Taylor-ovej teoreme. (Iste, kazdy co pouziva tuto metodu, dobre vie co sa od takych funnkciii vyzaduje).
Tak len niekolko prikladov.
a) [mathjax]e^x=1+\frac x{1!}+ \frac{x^2}{2!}+...+\frac{x^n}{n!}+... R=+\infty[/mathjax]
( ak niekomu treba podrobny popis ako sa k tomu pride, tak to tu pridam)
Analogicky mame rozzvoje pre [mathjax]\sin (x), \cos (x), sh( x), ch(x) ...[/mathjax].... atd. ( doplnte ....)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 05. 12. 2020 11:38 — Editoval vanok (30. 05. 2021 23:24)
Re: Rozvoj realne funkcie na mocninovy rad
Pripad 3), tu pojde o pouzitie derivacie.
Dam tu priklady ako pouzit vysledok z 1)
Mame [mathjax] \frac 1{1-x}= 1+x +x^2+ ... +x^n+... R=1[/mathjax]
Co da [mathjax] \frac 1{(1-x)^2}= 1+2x +3x^2+ ... (n+1)x^n+... R=1[/mathjax]
A aj [mathjax] \frac 1{(1-x)^3}= ....... R=1[/mathjax] ( doplnit)
Poroznyslajte aka teorema sa tu pouziva.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 05. 12. 2020 20:27
Re: Rozvoj realne funkcie na mocninovy rad
Pripad 4), pouzitie integracie.
Tu dam zasa len jednoduche priklady, kde sa vyuzije aj vysledok situacie 1).
Tento vysledok [mathjax] \frac 1{1-x}= 1+x +x^2+ ... +x^n+... R=1[/mathjax]
da [mathjax] \frac 1{1+x}= 1-x +x^2+ ... +(-1)^nx^n+... R=1[/mathjax]
A vdaka integracii ( podla akej teoremy?) dostaneme
[mathjax]\ln (1+x)=....[/mathjax]
[mathjax]\ln (1-x)=....[/mathjax]. (doplnte)
Tiez vdaka 1) lahko mame
[mathjax] \frac 1{1-x^2}= ...[/mathjax]
[mathjax] \frac 1{1+x^2}= ...[/mathjax] (doplnte)
A co da intégracia poslednych dvoch rozvojov?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 05. 12. 2020 20:30 — Editoval vanok (14. 01. 2021 12:31)
Re: Rozvoj realne funkcie na mocninovy rad
Pripad 5).
Tu bude troska podrobnejsie ukazany priklad, ako sa daju pouzit vhodne funkcionalne relacie.
Nech [mathjax]\alpha \in \Bbb R[/mathjax] a [mathjax]f:]-1;+\infty[\to \Bbb R, x \mapsto (1+x)^{\alpha }[/mathjax].
Lahko ukazeme, ze pre [mathjax]x \in ]-1;+\infty[[/mathjax] mame: [mathjax](1+x)f’(x)-\alpha f(x)=0[/mathjax] (*)
Predpokladajme, ze v okoli 0 mame: [mathjax]f(x)=a_0+a_1 x+...+a_nx^n+...[/mathjax]
Co plati o koeficientoch [mathjax]a_n[/mathjax]?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 06. 12. 2020 20:53
Re: Rozvoj realne funkcie na mocninovy rad
vanok napsal(a):
Mame [mathjax] \frac 1{1-x}= 1+x +x^2+ ... +x^n+... R=1[/mathjax]
Co da [mathjax] \frac 1{(1-x)^2}= 1+2x +3x^2+ ... (n+1)+x^n+... R=1[/mathjax]
A aj [mathjax] \frac 1{(1-x)^3}= ....... R=1[/mathjax] ( doplnit)
Tak už jsem to pochopil....
[mathjax] \frac d{dx} \frac 1{1-x} = \frac 1{(1-x)^2}[/mathjax]
[mathjax] \frac d{dx} \frac 1{(1-x)^2} = \frac 2{(1-x)^3} = 1 \cdot 2 + 2\cdot 3 x + 3 \cdot 4 x^2 + ...[/mathjax]
Offline
#14 14. 01. 2021 12:57 — Editoval vanok (15. 01. 2021 09:23)
Re: Rozvoj realne funkcie na mocninovy rad
Pozdravujem ↑ MichalAld:,
Ano,dobre si vyuzil naznaceny postup.
Analogicky to moze kazdy urobit v podobnych situaciach.
Ça sa tyka #12 ↑ vanok:, tak predpoklad, ze
[mathjax]f(x)=a_0+a_1x+...+a_ n x^n+...[/mathjax] v okoli 0, nam da
[mathjax]f^{\prime}(x)=[/mathjax] ( doplnte)
a operacie na mocninovych radoch daju pre [mathjax](1+x)f’(x)-\alpha f(x) =\sum_{n\ge0}b_nx^n[/mathjax] tieto rovnosti
[mathjax]b_0=-\alpha a_0+a_1[/mathjax]
[mathjax]b_1=-\alpha a_1+2a_2+a_1[/mathjax]
......
[mathjax]b_n=-\alpha a_n+(n+1)a_{n+1}+ na_n[/mathjax].
No vsak [mathjax]b_n=0[/mathjax] pre kazde n ( prava strana (*) v #12 je nulova) a tiez [mathjax]a_0=f(0)=1[/mathjax], konecne mame
[mathjax]a_n= \frac {\alpha(\alpha -1)...(\alpha-n+1)}{n!}[/mathjax].
Co da hladany rozvoj polomeru [mathjax]R=1[/mathjax]. (To R vam necham overit).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Rozvoj realne funkcie na mocninovy rad
