Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 11. 2020 13:47
Komplexná mocnina
Ahoj. Existuje pre každé reálne [mathjax]\alpha[/mathjax] vetva komplexnej funkcie [mathjax]f[/mathjax] komplexnej premennej definovanej predpisom[mathjax2]f{\left(z\right)}=z^{\alpha}[/mathjax2]
taká, že [mathjax2]\left(\forall x\in\mathbb{R}\right)\left(f{\left(\cos{\left(x\right)}+\mathrm{i}\sin{\left(x\right)}\right)}=\cos{\left(\alpha x\right)}+\mathrm{i}\sin{\left(\alpha x\right)}\right)[/mathjax2]?
MATH IS THE BEST!!!
Offline
- (téma jako vyřešené označil(a) jarrro)
#3 27. 11. 2020 05:10
Re: Komplexná mocnina
↑ MichalAld:Tiež tomu verím. Pre racionálne [mathjax]\alpha[/mathjax] to je Moivre a iracionálny exponent je v podstate predmetom mojej otázky, ale asi by sa mohla využiť spojitosť mocniny.
MATH IS THE BEST!!!
Offline
#4 27. 11. 2020 13:01 — Editoval MichalAld (27. 11. 2020 13:02)
Re: Komplexná mocnina
Problém je v tom, že exponenciální zápis komplexního čísla není jednoznačný, pokud
tak lze najít nekonečné množství různých x, které všechny dávají stejné z - imaginární exponenciála je periodická, takže ve skutečnosti je to
takže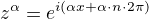
Pokud bude  celé číslo, tak se nic neděje, n krát celé číslo je zase celé číslo a výsledek je jen jeden.
celé číslo, tak se nic neděje, n krát celé číslo je zase celé číslo a výsledek je jen jeden.
Pokud bude  zlomek, tak může být výsledků více ... třeba když by to bylo 1/7, tak dostaneme 7 různých výsledků ... pro n = 0, 1, 2, ... 6. Potom už se to začne opakovat...
zlomek, tak může být výsledků více ... třeba když by to bylo 1/7, tak dostaneme 7 různých výsledků ... pro n = 0, 1, 2, ... 6. Potom už se to začne opakovat...
To odpovídá tomu, co známe z algebry, že polynom 7. stupně má 7 kořenů, či že 7. odmocnina může mít 7 různých výsledků.
Pokud bude  iracionální, tak se to pro žádné n nikdy nezačne opakovat a dostáváme nekonečné množství různých možných výsledků. Což použití obecné mocniny v komplexním oboru trochu komplikuje. Můžeme si samozřejmě jednu z těch hodnot vybrat jako nějakou "privilegovanou" - zpravidla tu, kde
iracionální, tak se to pro žádné n nikdy nezačne opakovat a dostáváme nekonečné množství různých možných výsledků. Což použití obecné mocniny v komplexním oboru trochu komplikuje. Můžeme si samozřejmě jednu z těch hodnot vybrat jako nějakou "privilegovanou" - zpravidla tu, kde  je v rozsahu 0 - 2*PI a problém tak odstranit.
je v rozsahu 0 - 2*PI a problém tak odstranit.
Při použití goniometrických funkcí je ten problém úplně stejný...
Offline
#5 27. 11. 2020 17:07
Re: Komplexná mocnina
teda na doplnenie to co pises tu ↑ MichalAld: je spravne a popiera to tvoj predchadzajuci pripevok,
cize aby sme to teda uzavreli, vysledna odpoved je: nie neda sa
Offline
#7 27. 11. 2020 19:06 — Editoval Brano (27. 11. 2020 19:10)
Re: Komplexná mocnina
↑ jarrro:
ano, na to je jednoduchy priklad na zaklade toho co hovoril ↑ MichalAld:
pre 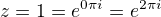
ty chces aby tvoja  (pre
(pre 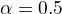 ) splnala
) splnala  a zaroven
a zaroven 
no a to je spor pre lubovolnu volbu  ak chces mat
ak chces mat  jednohodnotove
jednohodnotove
pre ine  to tiez zvladnes takto "pokazit", vynimkou su iba tie celociselne, kde to funguje ok
to tiez zvladnes takto "pokazit", vynimkou su iba tie celociselne, kde to funguje ok
vlastne cela idea toho ze si volis vetvu tej mocninovej multifunkcie je v tom, ze kedze sa tvoja vlastnost neda splnit pre  tak su splnme iba pre
tak su splnme iba pre  , alebo
, alebo ![kopírovat do textarea $x\in (\pi,3\pi]$](/mathtex/f2/f2438102234c3ee49cfecde672252ed4.gif) alebo nejaky iny polootvoreny interval s dlzkou
alebo nejaky iny polootvoreny interval s dlzkou 
a btw. cela multifunkcia je v nejakom zmysle spojita, ale kazda takato vetva je nespojita.
Offline
#8 28. 11. 2020 19:26
Re: Komplexná mocnina
↑ Brano:díky za odpoveď. Čiže je pravda, že pre každé reálne [mathjax]r[/mathjax] existuje vetva mocniny taká, že
[mathjax2]\left(\forall x\in \left[r, r+2\pi\right)\right)\left(f{\left(\cos{\left(x\right)}+\mathrm{i}\sin{\left(x\right)}\right)}=\cos{\left(\alpha x\right)}+\mathrm{i}\sin{\left(\alpha x\right)}\right)[/mathjax2]
?
MATH IS THE BEST!!!
Offline


 s
s  existuje jednoznacne
existuje jednoznacne  , take ze
, take ze  a potom mozes definovat
a potom mozes definovat  ; a
; a  sa doriesi podla
sa doriesi podla 