Matematické Fórum

↑ Placka03:

Keď sú presne 2 nepárne, zvyšné sú už automaticky párne - či?

Lze to řešit různě.

Tyto úvahy myslím vedou k jednoduchému řešení:

a) Házet najednou 6 kostkami dává stejný výsledek jako házet 6x jednou kostkou.
b) Sudé a liché číslo má stejnou pravděpodobnost.

Popřípadě ještě:
c) Sudé číslo můžeme brát jako výhru, liché jako prohru - nebo naopak.

↑ stodvacitka:

Mám dva druhy čísel - sudá a lichá. Na kostce jsou 3 sudá čísla a 3 lichá. Je tedy stejná pravděpodobnost, jestli padne sudé nebo liché číslo - tedy [mathjax]\frac{1}{2}[/mathjax].

Jelikož hážu šesti kostkami, obdržím nějakou šestici čísel dvou druhů. Mám tedy 64 možností.

Možností, ve kterých jsou 2 lichá a 4 sudá čísla, je [mathjax]P'(2, 4) = \frac{6!}{2! \cdot  4!} = 15[/mathjax].

Pravděpodobnost, že mi padne jedna z těchto možností tedy je [mathjax]\frac{15}{64} \approx 23,43\%[/mathjax].

Dá se také použít Bernoulliovo schéma:

Pravděpodobnost, že z [mathjax]n[/mathjax] nezávislých pokusů bude [mathjax]k [/mathjax] zdařilých, je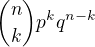



Házet jednou 6 kostkami dává stejný výsledek jako házet 6x jednou kostkou.
Za zdar můžeme třeba považovat, když "padle sudé číslo".

↑ stodvacitka:
Ještě k tvému prvnímu příspěvku.
Počet všech možností máš dobře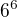
ale ty příznivě nikoli. Nejsou to kombinace s opakováním.
1) vybereš dvě kostky, na nichž padnou lichá čísla - to je 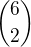možností.
2) Na každé vybrané kostce máš 3 možnosti pro lichá čísla (tj. 3*3)
3) a na zbylých čtyřech taky 3 možnosti pro sudá čísla (tj. 3*3*3*3)

pro pravděpodobnost ta dostáváš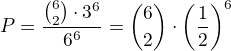


a to je totéž, co ti napsali v příspěvku #7