Matematické Fórum

Gauß69 · 25. 01. 2021 20:25

Pekny vecer prajem,

zadana je funkcia
[mathjax]u(x)=\frac{x}{|x|^\gamma} \ ,\ \gamma =\frac{n}{2}(1-\frac{1}{\sqrt{4(n-1)^2+1}}), \ \ x\in\mathbb{R}^n[/mathjax]

a tiez je zadana funkcia
[mathjax]A_{ij}^{\alpha \beta }(x)=\delta _{\alpha \beta }\delta _{ij }+((n-2)\delta _{\alpha i }+n\frac{x_\alpha x_i}{|x|})((n-2)\delta _{\beta j }+n\frac{x_\beta x_j}{|x|}) \ ,\ \ \ \ \ \ i,\ j,\ \alpha,\ \beta\in \{1,...,n\}[/mathjax]

Rad by som dokazal, ze pre [mathjax]\varepsilon \to 0[/mathjax] plati:
[mathjax]\int_{B_{2\varepsilon} } A_{ij}^{\alpha \beta }D_\beta u^j D_\alpha(\eta \varphi ^i) \to 0\ \ \ \ \ \ \forall\varphi \in C_0^\infty(B,\mathbb{R}^n)[/mathjax]

pricom
[mathjax]0<\varepsilon<\frac{1}{2}\ ,\ B_{2\varepsilon}=\{x\in\mathbb{R}^n: |x|<2\varepsilon\}\ [/mathjax]
a [mathjax]\eta [/mathjax] je vhodne zvolena cut-off funkcia s vlastnostou
[mathjax]\eta(x) \equiv 1, \ x\in B_\varepsilon[/mathjax] , a [mathjax]\eta(x) \equiv 0, \ x\in \mathbb{R}^n\setminus B_{2\varepsilon}[/mathjax]

Doteraz sa mi podarilo dokazat nasledujuce vlastnosti funkcii [mathjax]u[/mathjax] a [mathjax]A_{ij}^{\alpha \beta }[/mathjax]:
[mathjax]u\in W^{1,2}(B_1,\mathbb{R}^n)[/mathjax]
[mathjax]A_{ij}^{\alpha \beta }\in L^\infty(B_1)[/mathjax]
[mathjax]\lambda |\zeta |^2\le A_{ij}^{\alpha \beta }\zeta _\alpha^i\zeta _\beta^j\le M |\zeta |^2 \ \ ,\ \ \ \lambda ,\ M>0[/mathjax]

(Je to pisane s Einsteinovou sumacnou konvenciou)

Bati · 26. 01. 2021 00:22

Ahoj,
co na tom chces dokazovat? Pokud Du je v L^2, tak potom A Du D(eta phi) je take v L^2 (nezavisle na epsilon podle tveho zadani) a z Holderovy nerovnosti ten integral je mensi nez 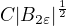$C|B_{2\varepsilon}|^{\frac12}$ . Btw. nezminil jsi jakou rovnici ta funkce resi, ale tipnul bych, ze neco jako div(|Du|^p A Du)=0.

Gauß69 · 26. 01. 2021 01:59

↑ Bati:
Ahoj Bati, dakujem za odpoved.
Funkcia [mathjax]u[/mathjax] by mala byt slabym riesenim systemu rovnic [mathjax]-D_\alpha (A_{ij}^{\alpha \beta }D_\beta u^j)=0\ \ \forall i\in\{1,...,n\}[/mathjax] na [mathjax]B_1[/mathjax].
Je to priklad od De Giorgi 1968.

Ako si sa prosim ta konkretne dostal k [mathjax]C|B_{2\varepsilon}|^{\frac{1}{2}}[/mathjax] ?

Ja to vidim s Holderovou nerovnostou tak, ze:
[mathjax]|\int_{B_{2\varepsilon} } A_{ij}^{\alpha \beta }D_\beta u^j D_\alpha(\eta \varphi ^i) |\le \max \|A_{ij}^{\alpha \beta }\|_{L^\infty}\cdot \int_{B_{2 \varepsilon} }|D_\beta u^j|\ |D_\alpha (\eta \varphi ^i)|[/mathjax]
[mathjax]\le \max \|A_{ij}^{\alpha \beta }\|_{L^\infty}\cdot \sqrt{\int_{B_{2\varepsilon} }|D_\beta u^j|^2}\sqrt{\int_{B_{2\varepsilon} }|D_\alpha (\eta \varphi ^i)|^2}=\max \|A_{ij}^{\alpha \beta }\|_{L^\infty}\cdot (2\varepsilon)^n\sqrt{\int_{B_1 }|D_\beta u^j|^2}\sqrt{\int_{B_1}|D_\alpha (\eta \varphi ^i)|^2}[/mathjax]
[mathjax]=(2\varepsilon)^n\max \|A_{ij}^{\alpha \beta }\|_{L^\infty}\|D_\beta u^j\|_{L^2}\|D_\alpha (\eta \varphi ^i)\|_{L^2}\to0[/mathjax]
Ak som nespravil v ziadnom kroku chybu, tak by aj toto malo riesit moj problem.

Otazne je len preco bolo treba pouzit cut-off funkciu [mathjax]\eta [/mathjax].
Kedze bolo potrebne dokazat, ze [mathjax]u[/mathjax] je slabym riesenim hore uvedeneho systemu, tak treba dokazat:
[mathjax]\int_{B_1 } A_{ij}^{\alpha \beta }D_\beta u^j D_\alpha\varphi ^i = 0\ \ \ \ \ \ \forall\varphi \in C_0^\infty(B,\mathbb{R}^n)[/mathjax]

V navode na riesenie je napisane, ze k [mathjax]\varepsilon \in(0,1/2)[/mathjax] treba zvolit cut-off funkciu [mathjax]\eta [/mathjax] so spomenutymi vlastnostami. Dalej treba vyuzit, ze [mathjax]\varphi =(1-\eta )\varphi +\eta \varphi [/mathjax]. A dalej treba vyuzit, ze [mathjax]u[/mathjax] je aj klasickym riesenim nasho systemu rovnic na [mathjax]B_1\setminus B_\varepsilon[/mathjax]. A nakoniec treba dokazat, ako som v prvom prispevku uviedol:
[mathjax]\int_{B_{2\varepsilon} } A_{ij}^{\alpha \beta }D_\beta u^j D_\alpha(\eta \varphi ^i) \to 0\ \ \ \ \ \ \forall\varphi \in C_0^\infty(B,\mathbb{R}^n)[/mathjax]

Chcem tym povedat, ze by som mohol hned pouzit, ze [mathjax]u[/mathjax] je klasickym riesenim na [mathjax]B_1\setminus B_\varepsilon[/mathjax]. A pre zvysny integral ponad [mathjax] B_\varepsilon[/mathjax] by som pouzila Holdera a islo by to k nule.
Preto si myslim, ze mi tu nieco nepasuje. Lebo takymto sposobom by som funkciu [mathjax]\eta [/mathjax] vobec nemusel pouzit ako stoji v navode.

Bati · 26. 01. 2021 13:24

Gauß69 napsal(a):
↑ Bati:
Ako si sa prosim ta konkretne dostal k [mathjax]C|B_{2\varepsilon}|^{\frac{1}{2}}[/mathjax] ?

Pokud $f\in L^2(B_1)$ , tak
$\int_{B_{\varepsilon}}|f|\leq\|1\|_{2,B_{\varepsilon}}\|f\|_{2,B_{\varepsilon}}\leq|B_{\varepsilon}|^{\frac12}\|f\|_{2,B_1}$ .

Aha, uz chapu co je vlastne zadani... no problem je v tom ,ze prave ten cut-off eta zavisi na epsilon. To by samo o sobe nevadilo, ale ty tam mas vlastne gradient tehle funkce, coz vyhodi 1/epsilon na tom mezikruzi, proto to nejde tak jednoduse odhadnout jak jsem napsal. Je potreba hezky rozderivovat ten soucin a odhadnout obe casti... kdyby to neslo, tak se jeste ozvi.

Gauß69 · 26. 01. 2021 14:12

Jaj, tak si myslel Holdera, uz je mi jasne.

Tu cut-off funkciu som potreboval, aby som mohol pouzit parcialnu integraciu na [mathjax]B_1\setminus B_{2\varepsilon}[/mathjax]. Lebo [mathjax](1-\eta)\varphi ^i [/mathjax] ma nulove okrajove podmienky na [mathjax]B_1\setminus B_{2\varepsilon}[/mathjax].

Este raz vdaka :)

Matematické Fórum

#1 25. 01. 2021 20:25

Regularita slabeho riesenia elliptickej sustavy diferencialnych rovnic

#2 26. 01. 2021 00:22

Re: Regularita slabeho riesenia elliptickej sustavy diferencialnych rovnic

#3 26. 01. 2021 01:59

Re: Regularita slabeho riesenia elliptickej sustavy diferencialnych rovnic

#4 26. 01. 2021 13:24

Re: Regularita slabeho riesenia elliptickej sustavy diferencialnych rovnic

Gauß69 napsal(a):

#5 26. 01. 2021 14:12

Re: Regularita slabeho riesenia elliptickej sustavy diferencialnych rovnic

Zápatí