Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 02. 2021 15:27
- check_drummer

- Příspěvky: 5181
- Reputace: 106
Součet vektorů
Ahoj, mějme půlkruh (s krajními body A,B) s jednotkovým poloměrem a se středem S, na tomto půlkruhu lichý počet bodů  . Dokažte, že
. Dokažte, že 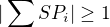 . (
. (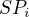 chápeme jako vektor a
chápeme jako vektor a  je norma.)
je norma.)
"Máte úhel beta." "No to nemám."
Offline
#2 27. 02. 2021 13:43 Příspěvek uživatele MichalAld byl skryt uživatelem MichalAld. Důvod: Je to blbost, co jsem napsal...
#3 27. 02. 2021 14:52
- check_drummer

- Příspěvky: 5181
- Reputace: 106
Re: Součet vektorů
↑ MichalAld:
Ahoj, proč chceš dosáhnout u příčné složky nulového součtu? Nějak nevidím, že z toho plyne požadované tvrzení.
"Máte úhel beta." "No to nemám."
Offline
#5 04. 03. 2021 20:26
Re: Součet vektorů
↑ check_drummer:
Ahoj, ja bych zacal s trema vektorama
Chceme ukazat, ze
coz lze upravit a zjednodusit na
Pouzitim souctoveho vzorce
coz je platna nerovnost, nebot argumenty vsech kosinu jsou z intervalu
Dal by se mohlo zkusit postupovat indukci, anebo provest stejny postup pro vice vektoru.
Offline
#6 11. 03. 2021 19:53
- check_drummer

- Příspěvky: 5181
- Reputace: 106
Re: Součet vektorů
Hodně stručně:
"Máte úhel beta." "No to nemám."
Offline
