Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 18. 03. 2021 11:55
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Lineární diferenciální rovnice 2. řádu
Zdravím,
je tá rovnica zapísaná správne? Pretože ak by mala opisovať pohyb nejakého pružinového oscilátora (vzhľadom na kontext zadania), tak by ten druhý člen mal byť v tvare [mathjax]kx[/mathjax] a nie [mathjax]k\dot{x}[/mathjax] a namiesto člena [mathjax]\ddot{x}[/mathjax] by som v rovnici očakával [mathjax]m\ddot{x}[/mathjax], kde [mathjax]m[/mathjax] je hmotnosť telesa daného oscilátora.
Offline
#3 18. 03. 2021 11:56 — Editoval Placka03 (18. 03. 2021 11:59)
Re: Lineární diferenciální rovnice 2. řádu
↑ Hafis:
Homogenní diferenciální rovnice druhého řádu se řeší tak, že se vytvoří charakteristický polynom levé strany tak, že se derivace nahradí mocninami, tedy v tomto případě takto:
[mathjax]\lambda ^2+k\lambda =0[/mathjax]
Toto vyřešíš jako kvadratickou rovnici:
[mathjax]\lambda(\lambda+k) =0[/mathjax]
[mathjax]\lambda_1 = 0, \lambda_2=-k[/mathjax]
X se potom rovná součtu součinů konstant s [mathjax]e^{\lambda t}[/mathjax], tedy
[mathjax]x=C_1e^{\lambda _1t}+C_2e^{\lambda _2t} = C_1e^{0t}+C_2e^{-kt} = C_1+C_2e^{-kt}[/mathjax]
Offline
#4 22. 03. 2021 18:36 — Editoval Hafis (22. 03. 2021 18:42)
Re: Lineární diferenciální rovnice 2. řádu
Omlouvám se, jedná se vskutku o rovnici: [mathjax]m\ddot{x}+k\dot{x}=0[/mathjax]
Došel jsem ke stejnému výsledku jako Placka03, akorát tedy jsem upravil výsledek o předchozí chybu v mém zápisu výchozí rovnice na: [mathjax]x = C_1+C_2e^{\frac{-k}{m}t}[/mathjax]
Mohl bych poprosit o další postup, jak určit konstanty [mathjax]C_{1}[/mathjax] a [mathjax]C_{2}[/mathjax]?
Offline
#6 22. 03. 2021 21:42
Re: Lineární diferenciální rovnice 2. řádu
Pokud je k tuhost pružiny, tak platí to co napsal Ferdish. Takto by bylo k koeficient tlumení, a popisovalo by to zhruba těleso pohybující se v nějakém prostředí, co klade odpor.
Navíc je v podstatě nesmysl to řešit jako rovnici druhého řádu, když z toho substitucí z=x' dostaneme rovnici prvního řádu...
Offline
#7 23. 03. 2021 18:50 — Editoval Hafis (23. 03. 2021 18:54)
Re: Lineární diferenciální rovnice 2. řádu
↑ žabí hněv:
Pokud  a
a  , pak je tedy
, pak je tedy  ?
?
Není možné, že mám zde chybu a mělo by to být tak, že 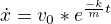 ?
?
Offline
#8 23. 03. 2021 19:52 — Editoval MichalAld (23. 03. 2021 19:52)
Re: Lineární diferenciální rovnice 2. řádu
Pokud
[mathjax]x = C_1+C_2e^{\frac{-k}{m}t}[/mathjax]
pak
[mathjax]x_{(0)} = C_1+C_2e^{\frac{-k}{m}0}=C_1+C_2[/mathjax]
A dále,
[mathjax]x' = \frac{-k}{m}C_2e^{\frac{-k}{m}t}[/mathjax]
takže
[mathjax]x'_{(0)} = \frac{-k}{m}C_2e^{\frac{-k}{m}0}=\frac{-k}{m}C_2[/mathjax]
Z toho se musejí určit ty konstanty.
Offline
 a
a 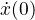 .
.