Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Téma zavřeno
- Hlavní strana
- » Základní škola
- » Úlohy o společné práci (TOTO TÉMA JE VYŘEŠENÉ)
#79 18. 12. 2007 20:14
Re: Úlohy o společné práci
1.den pracovala 1.dílna..................1/6 práce
2.den pracovala 1.dílna..................1/6 práce
za dva dny 1.dílna............... 2/6 práce
3.den 1. 2. dílna............................1/6 +1/9 práce........ 1 1
takto spolu pracovaly dílny .....x dní >> x * (----- + ----- )
6 9
sestavíme rovnici : 2 1 1
---- + ( ----- + ------) * x = 1
6 6 9
2 3x + 2x
------ + ---------- = 1 / *18
6 18
3*2 + 5x = 18
5x = 12
x = 2,4
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#81 19. 12. 2007 08:32
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Úlohy o společné práci
Frissone napsal(a):
V nabytkarskem podniku dostali zakazku na vyrobu zidli. V prvni dilne ne ni zacali pracovat v pondeli rano, v druhe az ve stredu rano. Kolik dnu budou obe dilny pracovat spolecne, jestlize v prvni dilne potrebuji na splneni zakazky 6 dnu a v druhe 9 dnu?
postupemmi to nevyšlo....
Jeste jednou se musim vratit k zadani a k reseni. Rovnice, jak navrhuje Frissone, je v naprostem poradku:
- za x je oznacena doba prace 1. dilny, x-2 - doba prace druhe dilny.
Z rovnice se vypocita x = 4,4.
A ted je jen potreba odecist 2, jelikoz doba, po kterou pracuji spolecne, je stejna jako doba, kdy pracovala 2. dilna. Prvni pracovala dele.
jelena napsal(a):
Editace - to je tak, kdyz se clovek zameri na detail - divala jsem se na rovnici, ale ne na zadani, to se omlouvam a opravuji:
vsechno vynasob 18 (i tu 1 - tam byva obvykle zapomenuto :-) - to plati i nadale a rovnice je tak, jak u vadi Ivana, kterou timto hezky zdravim :-)
Rovnice Ivany je samozrejme take v poradku a je z teto rovnice vypocitana primo doba prace druhe dilny, ktera je stejna jako doba spolecne prace.
Ted pujdu krasopisne napsat 50x "budu podrobne cist zadani" - ostatne uz jste nekdo dostal takovy trest?? - ja jsem ho dostavala docela casto a je opravdu ucinny - alespon na nejaky cas.
A vyuzivam moznost poslani pozdravu vam vsem :-)
Offline
#83 13. 01. 2008 19:56
Re: Úlohy o společné práci
Ahoj, prosim zejtra píšu velkou písemku z matiky a nic mi nejde vypočítat :'(
!!pan Šlapák jezdí do práce na kole.!!
Cesta do práce...15km/h
Cesta z práce...10km/h (protože je to do kopce)
A pan Šlapák tvrdí, že jeho průměrná rychlost je 12,5 km/h
Má pravdu??
Offline
#84 13. 01. 2008 20:20
Re: Úlohy o společné práci
Průměrná rychlost není aritmetický průměr, ale je to rychlost s jakou se pohybuje cyklista po celé dráze za celkový čas. 12,5km/h je aritmetický průměr z daných hodnot jednotlivých rychlostí.V tom případě nemá pravdu.
Budu-li, ale chtít vypočítat ar. průměr rychlostí, pak je odpověď správná. Záleží na úhlu pohledu. :-)
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#89 13. 01. 2008 20:47
Re: Úlohy o společné práci
Rovnoběžně s železniční tratí vede silnice. Po trati jede rychlostí 36km/h nákladní vlak. V opačném směru jede motocyklistka rychlostí 90km/h. Kolem vlaku projede za 3 s. Jak dlouhý je vlak?
Zápis:
vlak...36 km/h
motocyklista...90km/h
projede za......3 s.
délka vlaku.....x
Je to tak dobře??
Dál si nevím rady... Možná:
x x
-- + --- = 1 ???
36 90
Ale to mi příde trochu jako blbost.
Offline
#90 13. 01. 2008 21:00
Re: Úlohy o společné práci
jedině obecně : cesta do práce = cesta z práce .... 
15 t =10 ( t+x )
čas do práce je t a čas z práce je (t+x)..ten je delší protože cyklista se pohybuje menší rychlostí
a chceš-li vypočítat ar. průměr rychlostí : pak si vyjádříme 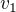 a
a 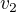


a tyto rychlosti sečteš a vydělíš dvěma a dostaneš : vp = 12,5+5x/t v km/h
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#94 13. 01. 2008 21:22
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Úlohy o společné práci
Pro Ivanu, srdecne zdravim :-)
Sla jsem se podivat po te ucebnici - mam od Fortuny, 9 ZS, ale rok 1991 (takovy priklad tam neni, asi jine vydani)
S tou cestou do kopce a dolu to je zajimave - ale pochybuji, ze by to takto pocitali na ZS - pomer rychlosti je 2/3, tj. pomer casu bude 3/2 Oznacime cas dolu za t, pak do kopce je 3/2t
10*1,5t + 15t 30t
prumerna rychlost = ----------------- = ------ = 12 km/hod
1,5t+t 2,5t
Ale opravdu nevim, zda je to postup pro ZS, co myslis?
Offline
#95 13. 01. 2008 21:31
Re: Úlohy o společné práci
↑ jelena: Zdravím :-)
Ano, mám také tuhle knížku a ted tady listuji a marně.Taky roč.1991.
Ty poměry rychlosí mne nenapadly.Pokud to bylo učitelem vysvětleno
pomocí poměru rychlostí, pak budiž.Ale učivo pro 9.roč.to není.Neuvádí
se ani ve fyzice.
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#96 13. 01. 2008 21:42
Re: Úlohy o společné práci
↑ Barbushqa: Z příkladů , jak jsem ti poslala já a Jelena je jasně vidět, jak se liší
průměrná rychlost, vypočítaná jako ar.průměr s rychlostí průměrnou, tak jak ji počítala Jelena.Aspoň
je na tomhle příkladě vidět, jak je důležité znát podstatu výpočtu po fyzikální stránce. :-)
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#97 17. 01. 2008 13:23
Re: Úlohy o společné práci
Dobrý den, mám spočítaných spoustu slovních úloh, ale zasekla jsem se na téhle:
Otec se synem by pokosili louku za 2 dny. Syn ovšem po prvním dnu musel odjet a otec zbytek louky dokončil za tři dny. Za kolik dní by každý z nich pokosil celou louku sám?
Můžete mi prosím poradit, jak sestavit rovnici? Děkuji
Offline
#99 17. 01. 2008 16:17
Re: Úlohy o společné práci
@Pavlinek: otec se synem pokosi louku za 2 dny. pokud dohromady pracuji jeden den a pak syn odjede, je jasne, ze behem jednoho dne pokosili prave polovinu louky, coz otec dodela (tj. dosece druhou pulku) sam za tri dny, tedy celou louku bude otec kosit 6 dni. pokud oba secou louku za dva dny, behem techto dvou dni otec posece prave jednu tretinu (za 6 dni ji posece celou, takze za dva dny je to tretina), tedy zbytek, to jest dve tretiny posece za dva dny syn, kdyz si to das do rovnice, tak zjistis, ze syn tu louku bude sict 3 dny.
Offline
#100 17. 01. 2008 16:34
Re: Úlohy o společné práci
↑ HRAD: Posílám : viz odkaz :
http://matematika.havrlant.net/forum/up … riklad.jpg :-)
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
Téma zavřeno
- Hlavní strana
- » Základní škola
- » Úlohy o společné práci (TOTO TÉMA JE VYŘEŠENÉ)
