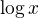Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Nenulový Lebesgueoův integrál Riemannovsky neintegrovatelné funkce
#1 05. 03. 2021 07:09
- Roscelinius
- Příspěvky: 51
- Škola: FEKT
- Reputace: 0
Nenulový Lebesgueoův integrál Riemannovsky neintegrovatelné funkce
Dobrý den,
dokázal by mi prosím někdo uvézt příklady funkcí které nejsou Riemannovsky integrovatelné ale mají nenulový integrál Lebesgueův? Ideálně kdyby šlo o funkce se vztyhem na fyziku.
Děkuji Petr
Offline
#2 05. 03. 2021 07:38
- mirek_happy24

- Místo: Praha
- Příspěvky: 156
- Škola: Gymnázium Na Pražačce
- Pozice: student
- Reputace: 6
- Web
Re: Nenulový Lebesgueoův integrál Riemannovsky neintegrovatelné funkce
Logicky si myslím, že to může být jakákoliv množina, s níž se můžeme setkat v praxi...
Doufám, že jsem Vám půomohl, nechěl bych přijít o reputaci.
Přeji hezký den.
INTELIGENTI SI ROZUMĚJÍ
Offline
#3 05. 03. 2021 08:31 Příspěvek uživatele vlado_bb byl skryt uživatelem vlado_bb. Důvod: nespravny pristup
#4 05. 03. 2021 09:54
- Roscelinius
- Příspěvky: 51
- Škola: FEKT
- Reputace: 0
Re: Nenulový Lebesgueoův integrál Riemannovsky neintegrovatelné funkce
↑ vlado_bb:
Dirichletova funkce má právě nulový L-integrál. V podstatě jsem narazil jen na funkce s nulovým L- integrálem, které nejsou R-integrabilní.
Neustále všude narážim na L-integral, tak zvažuji zda do něj hlouběji proniknout a hledám nějaké "praktické" (fyzikální) důvody. Na distribuce jsem se vždy díval jen technicky, tak úplně nedokážu posoudit, zda tam jen potřeba L-integral nebo stačí Riemannův.
Offline
#5 05. 03. 2021 11:06 Příspěvek uživatele vlado_bb byl skryt uživatelem vlado_bb. Důvod: nespravny pristup
#7 06. 03. 2021 14:28
- Richard Tuček

- Místo: Liberec
- Příspěvky: 1205
- Reputace: 19
- Web
Re: Nenulový Lebesgueoův integrál Riemannovsky neintegrovatelné funkce
Co takhle vzít funkci C + Dirichletova funkce
Offline
#8 10. 03. 2021 21:50
Re: Nenulový Lebesgueoův integrál Riemannovsky neintegrovatelné funkce
Ahoj ↑ Roscelinius:,
Bibliograficka poznamka :
Tu Theorems and Counterexamples in Mathematics
338 Pages ,
· English
by Bernard R. Gelbaum & John M.H. Olmsted
urcite nieco najdes.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 11. 03. 2021 00:05
Re: Nenulový Lebesgueoův integrál Riemannovsky neintegrovatelné funkce
Já tomu nějak speciálně nerozumím, ale myslel jsem, že funkce jako třeba ten zmíněný log(x), nebo třeba
Offline
#10 13. 05. 2021 12:58
- skipii1234

- Zelenáč
- Příspěvky: 3
- Škola: MFF UK
- Pozice: Student
- Reputace: 0
Re: Nenulový Lebesgueoův integrál Riemannovsky neintegrovatelné funkce
↑ Roscelinius:
Nejjednodušší funkce, co nejde Riemannem ale má nenulový Lebesgueův integrál, je "obrácená" Dirichletova funkce. f(x) = 0 pro x racionální a f(x) = 1 pro x iracionální. Takhle by ti integrál od 0 do 1 dal 1.
Jinak distribuce obecně je nějak zadefinovaná funkce, která požere známou funkci a vyhodí číslo. Když je to hezká distribuce, tak se dá i nějak reprezentovat v integrálním tvaru. Taková hezká je třeba Diracova delta distribuce  .
.
Asi by na většinu distribucí Lebesgueův integrál potřeba, ale při dokazování jejich vlastností se fakt hodí. Ten totiž má relativně slabé požadavky na prohození pořadí derivace, limity a sumy s integrálem. Riemannův je v tomto ohledu oproti Lebesgueovu integrálu dost nepraktickej. Dál třeba dělat Fourierovy řady a Fourierovu a Laplaceovu transformaci přes Riemanna by byl masochismus.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Nenulový Lebesgueoův integrál Riemannovsky neintegrovatelné funkce