Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 05. 2021 17:34 — Editoval Pozitron (29. 05. 2021 17:36)
Důkaz že pružina lze popsat pohybem po kružnici
Dobrý den, zrovna probíráme pružiny a zajímalo mě proč se odvozoval vztah[mathjax]y=y_{m}\sin (t\omega )[/mathjax] odvozován jako by se hmotný bod pohyboval po kružnici a zajímal mě důkaz že se tak ten bod opravdu pohybuje. Tedy udělat důkaz že todle platí [mathjax]y=y_{m}\sin (t\omega )[/mathjax]
můj důkaz:
síla pusobící je zjevně [mathjax]F=-ky[/mathjax] dosadíme do F=ma a dostanem [mathjax]a=-\frac{k}{m}y[/mathjax]
a taky víme že druhá derivace dráhy je zrychlení, označíme [mathjax]-\frac{k}{m}=l[/mathjax] a tak uděláme rovnici[mathjax]y\frac{\mathrm{d} y}{\mathrm{d}t }^{2}=ly[/mathjax]
řešením je [mathjax]y=C_{1}\mathrm{e}^{t\sqrt{l}}+C_{2}\mathrm{e}^{-t\sqrt{l}}[/mathjax]
teď by to chtělo asi nějaké podmínky a úpravy abych se dostal ke konečnému výrazu ale nevím si rady jak dále pokračovat napadlo mě že [mathjax]y(0)=0[/mathjax] a to by pak vyšlo že [mathjax]C_{1}=-C_{2}[/mathjax] ale potřebuji další určené hodnoty a tak prosím o radu jak to udělat.
(další nápad: využít tento vztah a nějak to zakomponovat do předchozí věci [mathjax]\omega =\frac{2\pi }{T}[/mathjax])
Offline
#2 29. 05. 2021 18:31
Re: Důkaz že pružina lze popsat pohybem po kružnici
↑ Pozitron:
Ještě si musíš určit podmínku pro počáteční rychlost.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 29. 05. 2021 19:53 — Editoval Pozitron (29. 05. 2021 20:16)
Re: Důkaz že pružina lze popsat pohybem po kružnici
↑ zdenek1:
Bohužel nejsem v tomdle vůbec zběhlý (je to první příklad který řeším) a tak netuším jak tam dát tu podminku na rychlost aby byla užitečná.
a jak tak uvažuji není i moje podmínka [mathjax]y(0)=0[/mathjax] nesmyslná, není smysluplnější podmínka [mathjax]y(0)=amplituda = y_{m}[/mathjax]?
možná dát podmínku [mathjax]y(0)=y_{m}[/mathjax] [mathjax]v(0)=0[/mathjax]
Offline
#4 29. 05. 2021 23:25
Re: Důkaz že pružina lze popsat pohybem po kružnici
↑ Pozitron:
Ano, podmínky 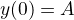 a
a 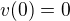 budou fungovat.
budou fungovat.
Stejně tak by fungovalo 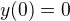 a
a 
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 30. 05. 2021 12:08
Re: Důkaz že pružina lze popsat pohybem po kružnici
↑ zdenek1:
Pořád nevím jak použít tu podmínku [mathjax]v(0)=0[/mathjax] jak použít podmínku [mathjax]y(0)=A[/mathjax] je mi celkem jasné dosadíme a vidíme [mathjax]C_{1}+C_{2}=A[/mathjax]
a taky vůbec netuším jak z toho můžu dostat ten tvar [mathjax]y=A\sin \omega t[/mathjax]
Offline
#6 30. 05. 2021 13:00
Re: Důkaz že pružina lze popsat pohybem po kružnici
↑ Pozitron:
spočítáš si první derivaci - to je rychlost, dostaneš (tvoje řešení pro  je špatně, zapomněl jsi na
je špatně, zapomněl jsi na  )
)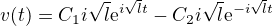
a po dosazení podmínky máš druhou rovnici 
Když určíš konstanty, použiješ identitu 
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#7 30. 05. 2021 13:09 — Editoval MichalAld (30. 05. 2021 13:13)
Re: Důkaz že pružina lze popsat pohybem po kružnici
Než použít rovnici ve tvaru co jsi zmínil, [mathjax]y\frac{\mathrm{d} y}{\mathrm{d}t }^{2}=ly[/mathjax] tedy [mathjax]y\frac{\mathrm{d} y}{\mathrm{d}t }^{2}-ly=0[/mathjax] je lepší psát rovnici ve tvaru [mathjax]y\frac{\mathrm{d} y}{\mathrm{d}t }^{2}+ly=0[/mathjax] nebo rovnou [mathjax]y\frac{\mathrm{d} y}{\mathrm{d}t }^{2}+ \omega^2 y=0[/mathjax].
Protože abychom dostali rovnici harmonického kmitání, musí tam být všude stejná znaménka (a přirozené je aby tam byla kladná). Pokud tam bude jedno plus a jedno minus, vede to na řešení dvou reálných exponenciál, a jedna z nich je "nestabilní", tj s rostoucím časem utíká k nekonečnu. Což rozhodně není harmonický oscilátor, a ani žádný jiný pasivní či konzervativní systém.
Jinak tvé otázce moc nerozumím. Protože odvozovat harmonické kmitání z kruhového pohybu se dělá dokud člověk nezná diferenciální rovnice. Potom už je to zbytečné, a v podstatě starost navíc. Takže moc nevím, co tě vlastně trápí, jestli to, jak se řeší ta rovnice harmonického kmitání (jak se z toho odvodí ten sinus), nebo to, jak to souvisí s rotačním pohybem.
Pokud jde o ta řešení...trik je v tom, že tam musí vyjít ta odmocnina ze záporného čísla, tedy [mathjax]\sqrt{-\omega^2} = \pm i \omega[/mathjax]. A součet dvou takovýchto exponenciál dává cosinus, rozdíl sinus, viz tady
Offline
#8 30. 05. 2021 13:25
Re: Důkaz že pružina lze popsat pohybem po kružnici
Jinak my jsme to ve škole dělali trochu jinak, než ukazuje zdenek, my jsme řešení ve tvaru
[mathjax]y = C_1 e^{-i\omega t} + C_2 e^{+i \omega t}[/mathjax]
ještě trošku upravili, než jsme začali dosazovat ty počáteční podmínky. S využitím poznatků z algebry je celkem zřejmé, že obecné řešení je superpozice dvou NEZÁVISLÝCH funkcí (v tomto smyslu lze funkce chápat jako vektory)...a tudíž když vyrobíme dvě NEZÁVISLÉ superpozice těchto funkcí, bude to také obecné řešení (akorát s jinými konstantami).
Takže volbou [mathjax]C_1 = -\frac{A}{2i}[/mathjax], [mathjax]C_2 = \frac{A}{2i}[/mathjax]
dostáváme [mathjax]y_A = A \sin (\omega t)[/mathjax]
a volbou [mathjax]C_1 = \frac{B}{2}[/mathjax], [mathjax]C_2 = \frac{B}{2}[/mathjax]
dostáváme [mathjax]y_B = B \cos (\omega t)[/mathjax]
(doufám, že to mám správně)
Takže nové obecné řešení (stejně dobré, jako to předchozí) je
[mathjax]y = A \sin (\omega t) + B \cos (\omega t)[/mathjax]
Případně, s využitím pravidel o práci s goniometrickými funkcemi a zavedením dalších dvou konstant můžeme dostat i
[mathjax]y = Y \sin (\omega t + \varphi)[/mathjax]
Je samozřejmě zajímavé, že ač původní rovnice i její konečné řešení je čistě reálné, při jeho hledání se moc neobejdeme bez komplexních čísel.
Offline
#9 31. 05. 2021 08:39
Re: Důkaz že pružina lze popsat pohybem po kružnici
↑ MichalAld:
Děkuji za odpověď, Jenom by mě zajímalo jak jste se dostal k [mathjax]\sqrt{l}=\sqrt{\frac{k}{m}}=\omega [/mathjax] . Pokud bychom mohli použít vzorec [mathjax]a=\omega ^{2}y[/mathjax] tak by to odvození bylo zjevné, ale to bychom museli první dokázat že bod na pružině se pohybuje po jakoby kruhové dráze ne?
Offline
#10 31. 05. 2021 08:46
Re: Důkaz že pružina lze popsat pohybem po kružnici
↑ MichalAld:
Zajímá mě jak to souvisí s rotačním pohybem. Nebyl jsem to schopen intuitivně pochopit a tak jsem to chtěl alespoň přes diferenciální rovnice odvodit ten vzorec a pak i pochopit.
Offline
#11 31. 05. 2021 09:46
Re: Důkaz že pružina lze popsat pohybem po kružnici
MichalAld napsal(a):
Než použít rovnici ve tvaru co jsi zmínil, [mathjax]y\frac{\mathrm{d} y}{\mathrm{d}t }^{2}=ly[/mathjax] tedy [mathjax]y\frac{\mathrm{d} y}{\mathrm{d}t }^{2}-ly=0[/mathjax] je lepší psát rovnici ve tvaru [mathjax]y\frac{\mathrm{d} y}{\mathrm{d}t }^{2}+ly=0[/mathjax] nebo rovnou [mathjax]y\frac{\mathrm{d} y}{\mathrm{d}t }^{2}+ \omega^2 y=0[/mathjax].
Jinak koukám, že jsem se nechal unést...rovnice má samozřejmě vypadat takto:
[mathjax]\frac{d^2y}{dt^2}+\omega^2y=0[/mathjax]
Ty předchozí zápisy jsou nesmysl...
Offline
#12 31. 05. 2021 09:50
Re: Důkaz že pružina lze popsat pohybem po kružnici
Pozitron napsal(a):
↑ MichalAld:
Děkuji za odpověď, Jenom by mě zajímalo jak jste se dostal k [mathjax]\sqrt{l}=\sqrt{\frac{k}{m}}=\omega [/mathjax] . Pokud bychom mohli použít vzorec [mathjax]a=\omega ^{2}y[/mathjax] tak by to odvození bylo zjevné, ale to bychom museli první dokázat že bod na pružině se pohybuje po jakoby kruhové dráze ne?
Pokud se chceme od harmonického oscilátoru dostat ke kruhovému pohybu, je to celkem snadné. Stačí vzít dvě pružiny a umístit je kolmo na sebe...jedna zařídí kmitání ve směru osy y, druhá ve směru osy x, a pokud budou vhodně fázově posunuté (o 90°) což lze zařídit vhodnými počátečními podmínkami, tak nám z toho vyjde kružnice, protože parametrická rovnice kružnice je prostě
[mathjax]y = \sin(\omega t)[/mathjax]
[mathjax]x = \cos(\omega t)[/mathjax]
Offline
#13 31. 05. 2021 09:57
Re: Důkaz že pružina lze popsat pohybem po kružnici
Pozitron napsal(a):
↑ MichalAld:
Děkuji za odpověď, Jenom by mě zajímalo jak jste se dostal k [mathjax]\sqrt{l}=\sqrt{\frac{k}{m}}=\omega [/mathjax] . Pokud bychom mohli použít vzorec [mathjax]a=\omega ^{2}y[/mathjax] tak by to odvození bylo zjevné, ale to bychom museli první dokázat že bod na pružině se pohybuje po jakoby kruhové dráze ne?
Né, tohle s kruhovou dráhou nesouvisí. Když máme diferenciální rovnici ve tvaru
[mathjax]\frac{d^2y}{dt^2}+\frac{k}{m}y=0[/mathjax]
a řešíme její charakeristický polynom, tak to je
[mathjax]\lambda^2+\frac{k}{m}[/mathjax]
[mathjax]\lambda^2 = -\frac{k}{m}[/mathjax]=0[/mj]
[mathjax]\lambda_{1,2} =\pm i \sqrt{\frac{k}{m}}[/mathjax]
Omegu tam v principu psát nemusíme vůbec, akorát si tím ušetříme práci, protože když nám pak vyjde, že
[mathjax]y=Y \sin( \sqrt{\frac{k}{m}} t + \varphi)[/mathjax]
tak víme, jaký je význam toho výrazu s odmocninou. Navíc v jiných oscilátorech tam vychází jiné kombinace veličin (l, g, L, C - podle toho, z čeho je oscilátor sestavený), a rovnice se řeší vždy stejně, jedno jaká písmenka tam napíšeme. Proto, když víme, co vyjde, tam můžeme psát rovnou omega^2 a ušetřit si tím trochu práce. S pohybem po kruhu to přímo nesouvisí ... asi tak, jak funkce sinus přímo nesouvisí s pohybem po kruhu. Je to prostě funkce s periodou 2*PI, proto musí mít v argumentu schované to 2*PI.
Offline
#14 31. 05. 2021 10:10 — Editoval MichalAld (31. 05. 2021 10:12)
Re: Důkaz že pružina lze popsat pohybem po kružnici
Proč se harmonický oscilátor připodobňuje k pohybu po kružnici jsem taky dříve moc nechápal ... ale když člověk nezná diferenciální rovnice, a zná pohyb po kruhu, tak lze ukázat, že ...
Při kruhovém pohybu je rychlost tečná na pohyb, tedy kolmá na polohový vektor. Zrychlení je pak zase kolmé na rychlost, tedy stejné jako polohový vektor, akorát opačným směrem.
Tedy pro kruhový pohyb platí, že
[mathjax]\vec{a} = -\omega^2\vec{r}[/mathjax]
[mathjax] \frac{d^2\vec{r}}{dt^2} = -\omega^2\vec{r}[/mathjax]
Což je tedy stejná rovnice jako pro harmonický oscilátor. Takto, je to vektorová rovnice, ale když jí rozepíšeme do složek, dostaneme dvě rovnice harmonických oscilátorů, jednu v ose x, druhou v ose y. A stejné rovnice mají i stejná řešení, takže řešení rovnice harmonického oscilátoru musí být stejné jako řešení rovnice kruhového pohybu (jeho průmětu třeba do osy y). A nepotřebujeme rozumět tomu, co jsou diferenciální rovnice druhého řádu a jak se přesně řeší. Nakonec je to docela šikovný trik.
Akorát že mě to třeba nikdy nikdo takto nevysvětlil, a shodu mezi kruhovým pohybem a závažím na pružině jsem bral jako čistě náhodnou.
Offline
