Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 17. 06. 2009 19:27
Re: Logaritmická funkce
určete D(f) http://forum.matweb.cz/upload/1245255977-equation.png[/img]
dekuji predem za pomoc
Offline
#4 17. 06. 2009 19:33
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Logaritmická funkce
↑ asim:Tož máme tam logaritmy. Argument logaritmu musí být kladný, základ také a navíc základ nesmí být 1. My máme základ vždy 2, takže přemýšlíme jen nad argumentem. Pro první závorku máme
3x-5>0, pro druhou
6x-12>0.
Žádná další omezení na x nemáme. Hledat D(f) tedy znamená zjistit, pro která x tyto dvě nerovnosti platí současně. Doporučuju obrázek číselné osy.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#6 17. 06. 2009 20:56
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Logaritmická funkce
↑ asim:Najdeme hodnoty x, pro které je x^2+6x+16=0. Zjistíme, že žádné takové nejsou. Protože nemá polynom x^2+6x+16 žádné reálné kořeny a protože má první koeficient kaldný, jedná se o parabolu "otočenou nahoru", která neprotíná osu x. Tato parabola je celá nad osou x, proto x^2+6x+16>0 pro všechna x, výraz log_7 (x^2+6x+16) je definován pro všechna x (základ kladný různý od 1, argument kladný vždy).
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#9 18. 06. 2009 18:38
- marnes

- Příspěvky: 11227
Re: Logaritmická funkce
↑ asim:
y=log_a\sqrt{x-3}+ log_a x^3
Tady jde zřejmě o určení def oboru. Uvědom si podmínku, kdy můžeme pracovat s logaritmem. To je když výraz je větší jak nula. Máme 2 logaritmy
1) odm(x-3)>0, to je kdyz (x-3)>0 a x>3
2) logx^3=3logx a podminka tedy x>0
z těcchto podmínek vytvoříš průnik. No a dále je podmínku pro základ
Jo. A na začátku vás zdravím.
Offline
#10 18. 06. 2009 18:41
- marnes

- Příspěvky: 11227
Re: Logaritmická funkce
↑ asim:
log(3x-5)+log(7x-3)=2+log 0,11
1)tady použij vlevo pravidlo pro součet logaritmů o stejném základu
2) vpravo 2=log100 a opět pravidlo o součtu
3) budeš řešit kvadr rovnici (3x-5).(7x-3)=11
4) nezapomeň na podmínky
Jo. A na začátku vás zdravím.
Offline
#11 18. 06. 2009 18:42
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Logaritmická funkce
↑ asim:Obvykle se používá trik, že když máme rovnici L=P, tak ji můžeme ekvivalentně upravit na  . V tomto případě
. V tomto případě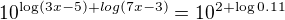
Použijeme vztah 

a logaritmy se zruší s exponenciálními fcemi:
EDIT: zpracována typografická připomínka kolegy Halogana.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#13 18. 06. 2009 20:01
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Logaritmická funkce
↑ halogan:Zdravím. No když už jsme u té typografie, celkem se držím toho, že věta začíná velkým písmenem, končí právě jedním interpukčním znamínkem a od další je oddělena mezerou, což je v poslední době na fóru mírný nadstandard. Zbytek tak nějak nechávám být. Nicméně díky za připomínku :)
EDIT: Aby to nebylo špatně vyloženo, nenarážím na typografii odpovědí, ale dotazů.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
