Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Schéma axiomů vydělení a univerzální třída (TOTO TÉMA JE VYŘEŠENÉ)
#1 09. 08. 2021 19:52
- Eratosthenes
- Příspěvky: 2592
- Reputace: 132
Schéma axiomů vydělení a univerzální třída
Zdravím,
Potřebuju trknout: Teorie množin (Balcar, Štěpánek):
Schéma axiomů vydělení
[mathjax]\forall a \exists z \forall x: x \in z \Leftrightarrow (x\in a \wedge \varphi (x))[/mathjax]
Chápu.
Definice univerzální třídy:
[mathjax]\bf V =\{y:y=y\}[/mathjax]
Chápu.
Věta: Univerzální třída není množina.
Důkaz sporem: [mathjax]\bf V[/mathjax] je množina v. Podle schématu vydělení existuje množina z, pro kterou platí:
[mathjax]\forall a \exists z \forall x : x \in z \Leftrightarrow (x \in a \wedge x\not\in x )[/mathjax]
Nechápu. Proč [mathjax]x\not \in x [/mathjax], když v tomto případě [mathjax]\varphi (x) [/mathjax] je [mathjax]x=x[/mathjax] ??
Budoucnost patří aluminiu.
Offline
- (téma jako vyřešené označil(a) Eratosthenes)
#2 09. 08. 2021 22:11
Re: Schéma axiomů vydělení a univerzální třída
Eratosthenes napsal(a):
Proč [mathjax]x\not \in x [/mathjax], když v tomto případě [mathjax]\varphi (x) [/mathjax] je [mathjax]x=x[/mathjax] ??
Protoze je to uzitecne. Zvolit si za [mathjax]\varphi (x) [/mathjax] formuli [mathjax]x=x[/mathjax] by bylo k nicemu. To bys akorat "dokazal", ze kdyz V je mnozina, tak V je mnozina.
Offline
#3 09. 08. 2021 23:19
- Eratosthenes
- Příspěvky: 2592
- Reputace: 132
Re: Schéma axiomů vydělení a univerzální třída
↑ Stýv:
Ale volbou [mathjax]x \not\in x[/mathjax] přece nedokážu, že [mathjax]\{ y: y = y \}[/mathjax] je vl. třída. Dokážu, že [mathjax]\{ y: y \not\in y \}[/mathjax] je vl. třída. OK, [mathjax]\{ y: y \not\in y \}[/mathjax] je podtřída [mathjax]\{ y: y = y \}[/mathjax], ale že nadtřída vl. třídy musí být vl. třída, to nikde předtím dokázáno není...
Budoucnost patří aluminiu.
Offline
#5 10. 08. 2021 07:15
- Eratosthenes
- Příspěvky: 2592
- Reputace: 132
Re: Schéma axiomů vydělení a univerzální třída
Já nijak. To dokázali Balcar se Štěpánkem: vydělení pro [mathjax]\{y:y \not\in y \}[/mathjax] dá [mathjax]z\in z \Leftrightarrow z\not\in z[/mathjax]. Jenže abych to dokázal pro [mathjax]\{y:y=y \}[/mathjax] , musím to dokázat ještě pro [mathjax]\{y:y \in y \}[/mathjax] a to nedokážu, protože to vede na [mathjax]z\in z \Leftrightarrow z\in z[/mathjax], což spor není.
Budoucnost patří aluminiu.
Offline
#6 10. 08. 2021 08:46
Re: Schéma axiomů vydělení a univerzální třída
↑ Eratosthenes: Ale vydeleni prece rika, ze [mathjax]\{y:y \not\in y \}[/mathjax] je mnozina.
Offline
#7 10. 08. 2021 09:45
- Eratosthenes
- Příspěvky: 2592
- Reputace: 132
Re: Schéma axiomů vydělení a univerzální třída
Předpokládáme, že univ. třída V je množina (ozn. v). Pak podle ax. vydělení existuje množina z
[mathjax]z=\{x:x \in v \wedge x\not\in x\}[/mathjax]
Odtud plyne [mathjax]z\in z \Leftrightarrow z \not\in z[/mathjax]
(Balcar, str. 49).
Až sem to chápu. Ale z toho má plynout, že univ. třída není množina. To nechápu. Podle mě je dokázáno, že množina není [mathjax]\{y:y \not\in y \}[/mathjax]. Ale má se to dokázat pro univerzální třídu, tj. pro [mathjax]\{y:y=y \}[/mathjax]...
Budoucnost patří aluminiu.
Offline
#8 10. 08. 2021 16:57
Re: Schéma axiomů vydělení a univerzální třída
Mozna uplne nerozumis dukazu sporem. Na zacatku neco predpokladas (V je mnozina) a na konci jsi dosel ke sporu ([mathjax]z\in z \Leftrightarrow z \not\in z[/mathjax]). Tedy predpoklad neplati a V neni mnozina.
Offline
#9 10. 08. 2021 18:30
- Eratosthenes
- Příspěvky: 2592
- Reputace: 132
Re: Schéma axiomů vydělení a univerzální třída
↑ Stýv:
Bez obav. Důkazu sporem rozumím docela dobře. Ještě jednou:
Univerzální třída je [mathjax]V=\{ x:\varphi (x)\} =\{ x: x=x\}[/mathjax].
Takže pro univerzální třídu je [mathjax]\varphi (x) \equiv (x=x)[/mathjax]
Předpokládám že V množina. Podle ax. vydělení musí existovat množina z
[mathjax]z=\{x:x \in v \wedge \varphi (x) \}[/mathjax]
Ještě jednou: [mathjax]\varphi (x)[/mathjax] je x=x. Takže kde se tam najednou vzalo [mathjax]x \not\in x [/mathjax] ??
Co je pro mě užitečné nebo neužitečné je šumák. Nemůžu přece jen tak místo x=x napsat [mathjax]x\not\in x[/mathjax] . Když potřebuju dokázat, že v každém trojúhelníku jsou shodné dva úhly, bude pro mě užitečné vzít místo všech jenom rovnoramenné a "dokážu" to. To je přece totéž a to nejde....
Budoucnost patří aluminiu.
Offline
#11 10. 08. 2021 20:22
- Eratosthenes
- Příspěvky: 2592
- Reputace: 132
Re: Schéma axiomů vydělení a univerzální třída
↑ Brano:
Žádná taková definice tam není.
Je tam:
Axiom vydělení
[mathjax]\forall a\exists z\forall x ( x\in z \Leftrightarrow x\in a \wedge \varphi (x))[/mathjax]
Tečka. O tom, jak má [mathjax]\varphi (x)[/mathjax] vypadat, nikde ani slovo.
Dále: Je-li univ třída množina, pak z toho axiomu prý plyne
[mathjax]z=\{x:(x\in v)\wedge(x\not\in x)\} [/mathjax]
Čili žádná definice. Plyne to prý z axiomu. A já nevím, proč nebo jak...
Budoucnost patří aluminiu.
Offline
#12 10. 08. 2021 20:38 — Editoval Brano (10. 08. 2021 20:45)
Re: Schéma axiomů vydělení a univerzální třída
Eratosthenes napsal(a):
Tečka. O tom, jak má [mathjax]\varphi (x)[/mathjax] vypadat, nikde ani slovo.
no ved to je prave ta pointa; ze to fi moze vyzerat ako len chceme; t.j. moze to byt lubovolna formula a [mathjax]\varphi (x) \equiv x \not\in x [/mathjax] je platna formula, tak si ju zvolime
to je ako ked mas vetu: ak je funkcia  diferencovatelna potom je
diferencovatelna potom je  spojita
spojita
tiez tam nie je povedane ako to  ma vyzerat a mysli sa tym ze
ma vyzerat a mysli sa tym ze  moze byt lubovolne a dosledkom tej vety je akekolvek tvrdenie, kde za
moze byt lubovolne a dosledkom tej vety je akekolvek tvrdenie, kde za  nieco dosadime; t.j, napriklad
nieco dosadime; t.j, napriklad
ak je funkcia  diferencovatelna, potom je
diferencovatelna, potom je  spojita
spojita
alebo
ak je funkcia 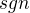 diferencovatelna, potom je
diferencovatelna, potom je 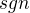 spojita
spojita
Offline
#13 10. 08. 2021 22:15
- Eratosthenes
- Příspěvky: 2592
- Reputace: 132
Re: Schéma axiomů vydělení a univerzální třída
>> no ved to je prave ta pointa; ze to fi moze vyzerat ako len chceme; t.j. moze to byt lubovolna formula a [mathjax]\varphi (x) \equiv x\not\in x[/mathjax] je platna formula, tak si ju zvolime..
OK. Ale [mathjax]\varphi (x) \equiv x\in x[/mathjax] je taky platná formule. A když si ji zvolím, "dokážu", že univ. třída je množina...
Dále: já mám větu dokázat a ne ověřovat její platnost konkrétními příklady.
Vezmu třeba ty diferencovatelné funkce. Mám dokázat větu: ak je funkcia  diferencovatelna potom je
diferencovatelna potom je  spojita
spojita
Podle Tebe je důkazem toto: Funkce může vypadat, jak jen chceme, takže to může být libovolná diferencovatelná funkce.  je platná funkce. Je diferencovatelná, takže dokážu, že je spojitá a důkaz je hotov.
je platná funkce. Je diferencovatelná, takže dokážu, že je spojitá a důkaz je hotov.
No to snad ne.
Za třetí: [mathjax]\varphi (x)[/mathjax] není v tomto případě libovolná formule. Mám dokázat nějaké tvrzení o univerzální třídě. Formule, která ji definuje, je x=x a nic jiného. Tam žádná libovůle není.
Budoucnost patří aluminiu.
Offline
#14 10. 08. 2021 22:41
Re: Schéma axiomů vydělení a univerzální třída
Eratosthenes napsal(a):
OK. Ale [mathjax]\varphi (x) \equiv x\in x[/mathjax] je taky platná formule. A když si ji zvolím, "dokážu", že univ. třída je množina...
Kdyz si zvolis [mathjax]\varphi (x) \equiv x\in x[/mathjax], nedojdes ke sporu, takze nic nedokazes.
Eratosthenes napsal(a):
Za třetí: [mathjax]\varphi (x)[/mathjax] není v tomto případě libovolná formule. Mám dokázat nějaké tvrzení o univerzální třídě. Formule, která ji definuje, je x=x a nic jiného. Tam žádná libovůle není.
Ale my nechceme psat definici univerzalni tridy. My chceme z univerzalni tridy vydelit nejakou jeji podmnozinu, ktera nas privede ke sporu.
Offline
#15 10. 08. 2021 22:58
Re: Schéma axiomů vydělení a univerzální třída
zda sa mi z hovoris trosku scesty, skus citat co som napisal
veta "ak je funkcia  diferencovatelna potom je
diferencovatelna potom je  spojita" je patna avsak o jej dokaze sme sa vobec nebavili, ale bavili sme sa o jej dosledkoch; treba spravne citat "smer sipky" v implikacii
spojita" je patna avsak o jej dokaze sme sa vobec nebavili, ale bavili sme sa o jej dosledkoch; treba spravne citat "smer sipky" v implikacii
rovnako ako sa nebavime o platnosti axiomy vydelenia, ale o jej dosledkoch
co sa teda tyka toho konkretneho dokazu tak zacinam mat pocit ze sa snazis iba trolit, ale skusme este raz
axioma: [mathjax]\forall a \exists z \forall x: x \in z \Leftrightarrow (x\in a \wedge \varphi (x))[/mathjax]
niekolko jej dosledkov
[mathjax]\forall a \exists z \forall x: x \in z \Leftrightarrow (x\in a \wedge x=x)[/mathjax]
[mathjax]\forall a \exists z \forall x: x \in z \Leftrightarrow (x\in a \wedge x\in x)[/mathjax]
[mathjax]\forall a \exists z \forall x: x \in z \Leftrightarrow (x\in a \wedge x\not\in x)[/mathjax]
vsetko su to platne tvrdenia, lebo vyplivaju z vyssie uvedenej prostym dosadenim za fi
a mozno si si niekedy uz vsimol ze v dokaze nejakej vety nemas predpisane ktore tvrdenia mozes a ktore nemozes pouzivat; mozes pouzit lubovolne tvrdenie, za predpokladu, ze je platne (resp. dokazane z axiom) a konkretne si mozes teda zvolit, ze pouzijes to posledne tvrdenie, ako sa rozhodli autori. Potom urobili dosledok tohoto tvrdenia kde dosadili V za a, co mohli urobit, lebo predpokladali, ze V je mnozina. Kedze tym dospeli k sporu, tak z toho usudili, ze ten predpoklad nemoze byt spravny ako nam hovori metoda dokazu sporom.
Offline
#16 11. 08. 2021 07:31
- Eratosthenes
- Příspěvky: 2592
- Reputace: 132
Re: Schéma axiomů vydělení a univerzální třída
↑ Stýv:
↑ Brano:
No vidíte, hoši - to, co jste napsali jako poslední, jste měli napsat na začátku a bylo by hotovo. Konečně jsem to pochopil :-)
To nebylo o trolení, fakt jsem tomu nerozuměl. Už to chápu, takže díky.
Budoucnost patří aluminiu.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Schéma axiomů vydělení a univerzální třída (TOTO TÉMA JE VYŘEŠENÉ)
