Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 06. 2009 18:20
součet řady
Řada: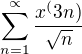
-označte s(x) funkční hodnoty součtu řady v K (oboru konvergence) a určete hodnotu čísla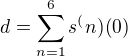
jde o n-tou derivaci z s v bodě 0.
Ze zadání jsem jsem moc nepochopila, co mám dělat. Můžete mi někdo, prosím, popsat postup možného řešení? Předem děkuji za pomoc.
Offline
#2 21. 06. 2009 22:33 — Editoval Marian (21. 06. 2009 22:33)
Re: součet řady
↑ misickacz:
Nejprve k zápisu v TeXu ... Pokud chceš mít c exponent více než jeden objekt, je potřeba exponent uzavřít do složených závorek, tedy třeba a^{x+y} dává 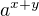 . Tvé použití dává pak chybu (v exponentu je pouze první část). Řada, o kt. nám jde je patrně (pokud to správně čtu) tato
. Tvé použití dává pak chybu (v exponentu je pouze první část). Řada, o kt. nám jde je patrně (pokud to správně čtu) tato
Pokud dále správně chápu, má symbol s(x) označovat součtovou funkci na oboru konvergence K. Co označuje 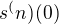 . Má být správně
. Má být správně 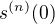 , tj. derivace? Pak by řešení úlohy nemělo dělat problém.
, tj. derivace? Pak by řešení úlohy nemělo dělat problém.
Je nutné si uvědomit, že na oboru konvergence potenční řady je možné derivovat nekonečnou řadu člen po členu. Tj. bude:
Podobně se ukáže, že i druhá derivace v nule je nulová. Uvědomíš si to třeba tak, že si napíšeš první dva členy původní řady, tj. (x^3)/(sqrt(1))+(x^6)/(sqrt(2))+... Potom je jasné, že třetí derivace bude rovna s''(0)=6. čtvrtá a pátá derivace bude zase nulová a šestou spočítáš jistě sama podobně. Sečtením těchto šesti čáísel dostaneš požadovanou hodnotu čísla "d".
Offline
