Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » pravděpodobnost P(X+Y<1,5) (TOTO TÉMA JE VYŘEŠENÉ)
#2 22. 06. 2009 03:49 — Editoval autocont (22. 06. 2009 10:18)
Re: pravděpodobnost P(X+Y<1,5)
Ahoj,
zkus si nakreslit obrázek, jak vypadá X+Y<1,5... je to trojúhelníček vymezený osami x a y a přímkou y=1,5-x. Zbývá stanovit jednotlivé rozsahy na osách:
0 <= x <= 1,
0 <= y <= 1,5-x
a v těchto mezích zintegrovat zadanou funkci 1/3 * (x+y) .
Kdyby to bylo špatně, tak mě někdo opravte :)
A jeste mě napadlo, jak by se počítalo, kdyby v zadání bylo třeba P(X < 0,5). Dělalo by se to přes jednoduchý integrál nebo dvojný? Děkuju
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » pravděpodobnost P(X+Y<1,5) (TOTO TÉMA JE VYŘEŠENÉ)
 pro 0<x<1, 0<y<2
pro 0<x<1, 0<y<2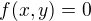 jinak
jinak