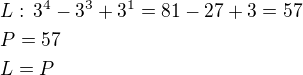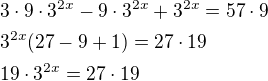Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Exponenciální rovnice - Jak na ni :o) (TOTO TÉMA JE VYŘEŠENÉ)
#2 09. 07. 2009 12:29 — Editoval halogan (09. 07. 2009 12:32)
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Exponenciální rovnice - Jak na ni :o)

Teď uděláme tři věci:
1) Rozepíšeme si 3^{...} tak, abychom oddělili neznámou od konstant v exponentech. Např.: 
2) Sečteme tyto výrazy ( ) jako jablka.
) jako jablka.
3) Přepíšeme si pravou stranu tak, aby tam nějak figurovala trojka (nepovinné, ale bude se to nejspíš hodit). V tomto případě 3*19.
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Exponenciální rovnice - Jak na ni :o) (TOTO TÉMA JE VYŘEŠENÉ)