Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 01. 2008 21:46
- v.bohuslav
- Zelenáč
- Příspěvky: 10
- Reputace: 0
Dvě rovnice
Potřeboval bych helpnout s 2 rovnicema
1. x-log(x-1) = 0 (logaritmus je pri zaklade 10)
2. x+e^x = 0
jsem nejak mimo a nedokazu s tim pohnout.
Offline
#4 15. 01. 2008 00:39
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Dvě rovnice
První se dá řešit i takto: převedeme na tvar
e^x=x-1, přitom ale pro x>0
e^x>x+1, takže aby platila zadaná rovnice, muselo by být x-1>x+1, což nelze.
Druhá rovnice řešení bohužel má, určit ho bez W(x) neumím (a s W(x) taky ne, ale to jednou se to možná naučím).
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#5 15. 01. 2008 08:38 — Editoval Marian (15. 01. 2008 08:59)
Re: Dvě rovnice
Obe dve tyto rovnice maji reseni, jez se da vyjadrit pomoci Lambertovy funkce W(x). Ukazu, jak je vyresit ...
ad 2)
Podobne v pripade 1).
ad 1)
Mala poznamka zaverem: Na funkci W(x) jsem pohlizl jako na funkci komplexni promenne, tedy snad by bylo nejlepsi psat W(z). Zajemce bych chtel upozornit na tzv. Eisensteinovu nekonecnou vez z mocnin (souvisi s pojmem tetrace cisla). Kdykoliv totiz "nekonenca vez" 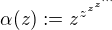
konverguje, pak plati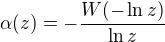 .
.
Offline
#6 15. 01. 2008 13:06
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Dvě rovnice
Díky za vysvětlení. Zkoušel jsem kdysi řešit rovnici 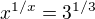 a Maple na mě vychrlil nějaké W funkce. Teď už aspoň vím, jak to udělal.
a Maple na mě vychrlil nějaké W funkce. Teď už aspoň vím, jak to udělal.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
 .
.