Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 03. 2017 10:53
- No Brain Kid

- Zelenáč
- Příspěvky: 11
- Škola: SZŠ Ruská
- Pozice: student
- Reputace: 0
Parametrická rovnice
Dobrý den.
Mám dva problémy s parametrickými rovnicemi. Vyřešil jsem je, ale jen protože byla nápověda ve výsledcích (abcde)
Nevím co bych dělal bez toho.
1) Určete hodnotu reálného parametru p tak, aby alespoň jedno řešení rovnice bylo kladné reálné číslo. 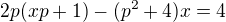
2) Určete všechny hodnoty reálného parametru p, pro které má následující rovnice právě dva různé reálné kořeny. 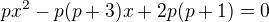
Offline
#2 15. 03. 2017 11:14
Re: Parametrická rovnice
↑ No Brain Kid:
1) vyjádři si  a pak polož
a pak polož  a dopočítej
a dopočítej
2) za určitých podmínek (jakých) se jedná o kvadratickou rovnici. Kdy má kvadratická rovnice dva různé reálné kořeny?
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 15. 03. 2017 12:37 — Editoval No Brain Kid (15. 03. 2017 12:52)
- No Brain Kid

- Zelenáč
- Příspěvky: 11
- Škola: SZŠ Ruská
- Pozice: student
- Reputace: 0
Re: Parametrická rovnice
↑ zdenek1: 2) Doufám, že toto je správný postup. 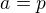
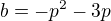
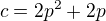
tudíž 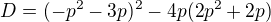
kvadratická rovnice má dvě řešení, když  takže po úpravě jsem dostal rovnici
takže po úpravě jsem dostal rovnici 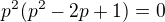 a z toho jsem došel k intervalu
a z toho jsem došel k intervalu 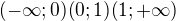
1) U tohoto příkladu jsem se zasekl u 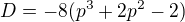 a nevím jak to dál upravit. Další postup by pak byl najít
a nevím jak to dál upravit. Další postup by pak byl najít  a
a  ale nevím jak to upravit.
ale nevím jak to upravit.
Děkuji za pomoc zdenku1 :)
Offline
#4 15. 03. 2017 12:39 Příspěvek uživatele No Brain Kid byl skryt uživatelem No Brain Kid. Důvod: Dvakrát jsem odeslal ten samý příspěvek
#5 15. 03. 2017 13:17
Re: Parametrická rovnice
↑ No Brain Kid:
2) je dobře.
1) to není kvadratická rovnice, takže proč počítáš nějaký diskriminat?
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#6 15. 03. 2017 14:08
- No Brain Kid

- Zelenáč
- Příspěvky: 11
- Škola: SZŠ Ruská
- Pozice: student
- Reputace: 0
Re: Parametrická rovnice
↑ zdenek1: 1) Aha.... Já smíchal dva příklady dohromady >.<
I tak je tam jedna věc které nerozumím:
Upravím si vzorec na 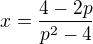 a protože
a protože  tak
tak  a když vyšetřuji 4-2p ≠ 0 tak mi vyjde p≠2 přitom správný interval je
a když vyšetřuji 4-2p ≠ 0 tak mi vyjde p≠2 přitom správný interval je 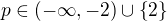 když dosadím 2 do původní rovnice, tak mi vyjde, že má nekonečně mnoho řešení, ale nenapadlo by mě vyšetřovat 2, když z podmínky to nesmí být. Jaký je k tomu myšlenkový pochod?
když dosadím 2 do původní rovnice, tak mi vyjde, že má nekonečně mnoho řešení, ale nenapadlo by mě vyšetřovat 2, když z podmínky to nesmí být. Jaký je k tomu myšlenkový pochod?
Offline
#7 15. 03. 2017 14:13 — Editoval misaH (15. 03. 2017 14:23)
- misaH
- Příspěvky: 13467
Re: Parametrická rovnice
↑ No Brain Kid:
No.
Myšlienkový pochod je taký, že parameter môže byť ľubovoľné číslo.
Ak s ním máš počítať ďalej, musíš rozlišovať.
Vo všeobecnosti parametrom nedelíš, ale vyrobíš rovnicu s jednou stranou rovnou nule a skúsiš na druhej strane urobiť súčin.
A vždy sa treba vrátiť k otázke úlohy.
Offline
#8 15. 03. 2017 15:36
- No Brain Kid

- Zelenáč
- Příspěvky: 11
- Škola: SZŠ Ruská
- Pozice: student
- Reputace: 0
Re: Parametrická rovnice
↑ misaH: Takže kdybych to řekl polopatě, tak mám zkusit dosadit podezřelá čísla?
Offline
#9 15. 03. 2017 17:07 — Editoval misaH (15. 03. 2017 17:08)
- misaH
- Příspěvky: 13467
Re: Parametrická rovnice
↑ No Brain Kid:
No - ani nie. Píšem to...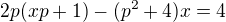
.
.
.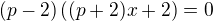
Ak by p bola 0, tak by riešením boli všetky reálne čísla.
Ako znela otázka v úlohe?
Offline
#10 16. 03. 2017 11:59
- No Brain Kid

- Zelenáč
- Příspěvky: 11
- Škola: SZŠ Ruská
- Pozice: student
- Reputace: 0
Re: Parametrická rovnice
↑ misaH: p nula být nemůže, ale už to asi uvidím z tvé úpravy :) V podstatě když p = 2 tak pak 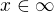 a z podmínky která je v zadání, tak
a z podmínky která je v zadání, tak 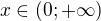 . Může být?
. Může být?
Offline
#11 16. 03. 2017 13:27
Re: Parametrická rovnice
↑ No Brain Kid:
Zdravím,
zdá se mi, že závěr tvého řešení spíše odhaduješ. Podobné úvahy, jaké je třeba provést zde, jsi už řešil ve svém tématu
Je třeba dořešit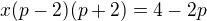
a) p=2 ......
b) p=-2 .....
c) 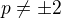 .....
.....
Offline
#12 16. 03. 2017 19:09 — Editoval misaH (16. 03. 2017 19:09)
- misaH
- Příspěvky: 13467
Re: Parametrická rovnice
↑ No Brain Kid:
Myslím, že je pre teba neznáma základná vec.
Parameter totiž môže byť KAŽDÉ číslo.
Nemôžeš povedať, že parameter niektoré číslo nie je.
Ako píše Al1 (zdravím :-) ). Musíš uvážiť aj to, ako bude vyzerať riešenie pre - podľa teba - "nevhodné" p.
Pričom riešením je napríklad aj to, že riešenie neexistuje.
Musíš prejsť VŠETKY hodnoty parametra.
Offline
#13 28. 05. 2024 21:18
Re: Parametrická rovnice
Pro příklad 2 je velmi vhodný první krok podělení [mathjax]p[/mathjax]. Kvůli tomu je potřeba si uvědomit, že tak lze učinit pouze pro [mathjax]p\neq 0[/mathjax].
Čili případ [mathjax]p=0[/mathjax] musíme vyšetřit zvlášť (dosadíme a vyjde nám [mathjax]0=0[/mathjax]) a zjistíme, že rovnice pak má nekonečně mnoho řešení. Tedy aby rovnice měla 2 řešení, nesmí být [mathjax]p=0[/mathjax].
Dále je potřeba pořešit zbývající kvadratickou rovnici a zjistit, kdy má 2 reálná řešení (diskriminant větší než 0).
Offline
#15 29. 05. 2024 06:27 — Editoval misaH (29. 05. 2024 06:27)
- misaH
- Příspěvky: 13467
Re: Parametrická rovnice
↑ andowero:
Plus na tomto fóre sa nepreferuje kompletné riešenie. Treba si prečítať pravidlá fóra, a to s porozumením.
Snažíme sa pomáhať, t. j. posúvať zadávateľa návodnými otázkami, aby mohol z čo najväčšej časti vyriešiť úlohu sám.
Exhibicionizmus sa tu nepestuje, je to proti pravidlám fóra.
Offline