Matematické Fórum

lukaszh · 14. 04. 2009 16:19

Inšpiroval ma jeden príspevok zo základnej školy. Myslíte si, že nekonečno je vôbec číslo? Alebo rozdeľujeme nekonečno na komplexné nekonečno alebo reálne nekonečno? Som zvedavý na názory.

Kondr · 14. 04. 2009 16:44

Než položíme otázku "je nekonečno číslo?" je nutné si položit otázku "co je to číslo". Pokud si řekneme, že číslo je libovolné komplexní číslo (což je IMHO rozumná odpověď), pak nekonečno číslo není. Všimni si, že to co jsem napsal není definice kruhem. Pojem "komplexní číslo" je definován pomocí pojmu "reálné číslo", ten pomocí pojmu "racionální číslo", ten pomocí pojmu "přirozené číslo" a k definici přirozeného čísla nám stačí pojmy množina, prázdná množina a sjednocení.

V souvislosti s limitami se často používá množina 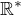$\mathbb{R}^*$ , která je definovaná jako 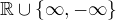$\mathbb{R}\cup\{\infty,-\infty\}$ . Jistě by šlo podobně definovat množinu $\mathbb{C}^*$ (komplexní analýzu jsem neměl, tak nevím, jestli se to standardně dělá). Pokud bychom použili některou z těchto množin v definici pojmu číslo, tak nekonečno číslem bude.

Je také potřeba vzít v potaz, že v předchozím odstavci jsem mluvil o potenciálním nekonečnu. Má smysl se ale bavit o aktuálním nekonečnu, tedy o kardinalitách množin 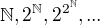$\mathbb{N},2^{\mathbb{N}},2^{2^{\mathbb{N}}},...$ .
To jsou kardinální čísla. A máme opět otázku: jsou kardinální čísla čísla?

Mephisto · 22. 08. 2009 21:38

Tak tohle je podle mého názoru tak trochu hraní si se slovíčky :)

Máme jasně definované číselné množiny
N, Z, Q, R, C
přičemž nekonečno triviálně není prvkem ani jedné z nich.

Pak máme třídu všech kardinálních čísel, a třídu všech ordinálních čísel, přičemž nejmenším nekonečným kardinálem je Aleph0, který vyjadřuje mohutnost množiny přirozených čísel, ... ovšem nekonečnem bych teda Aleph0 nenazval

a nejmenším nekonečným ordinálem je omega, ovšem nazvat omega "nekonečnem" je dle mého názoru taky silně nepřesné.

Čili, nekonečno prostě není číslo z žádnoho standardního pohledu, a tečka :)

gladiator01 · 22. 08. 2009 21:53

Třeba by někoho zajímalo: http://www.scienceweek.cz/search.php (http://media.rozhlas.cz/leonardo/audio/ … 885688.mp3)

Olin · 22. 08. 2009 22:01

↑ Mephisto:

Přesně jak říkáš, jde jen o hraní se slovíčky, já bych třeba zase váhal nad tím, jestli nazvat $\aleph_0$ číslem.

V kontextu např. operací s množinou 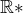$\mathbb{R}*$ bych se nekonečno nazvat číslem neštítil. Je to prostě prvek rozšířené množiny reálných čísel, je to tedy číslo.

Mephisto · 22. 08. 2009 22:08

↑ Olin:

jj, ... ale mě se tahle množina R* moc nelíbí :( Není to těleso, (R*, +) není grupa... (R*-{0}, *) není taky grupa... ta struktura má dva prvky, které se při násobení chovají jako nula, totiž nula a nekonečno...

prostě z algebraického hlediska je to nehezké :) Ovšem pokud si je člověk těchto neduhů vědom, tak proč to v opodstatněných případech nepoužívat, že... :)

Matematické Fórum

#1 14. 04. 2009 16:19

N, Z, Q, R, C a nekonečno

#2 14. 04. 2009 16:44

Re: N, Z, Q, R, C a nekonečno

#3 22. 08. 2009 21:38

Re: N, Z, Q, R, C a nekonečno

#4 22. 08. 2009 21:53

Re: N, Z, Q, R, C a nekonečno

#5 22. 08. 2009 22:01

Re: N, Z, Q, R, C a nekonečno

#6 22. 08. 2009 22:08

Re: N, Z, Q, R, C a nekonečno

Zápatí