Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 04. 2009 09:10
Rada - zajímavá úloha
Ahoj,
mám tady docela zajímavou úlohu a nevím si s ní rady. Pokud byste věděli jak nato nebo měli nějakou radu dejte určitě vědě budu vám vděčný.
Takže k zadání:
Máme 4 rakety v rozích čtverce o straně a. Každá raketa je namířena na raketu před sebou. V jeden časový okamžik všechny rakety vyletítí konstantní rychlostí v (žádné zrychlení) a stále míří na raketu před sebou.
Otázkou je jakou budou mít trajektorii (vypočíst ji) a za jak dlouho po startu se srazí?
Obrázek:
0..............................................................................00
0 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. 0
00..............................................................................0
(00 - je raketa namířená na raketu před sebou)
Takhle nějak by to mělo zhruba vypadat po odpálení raket:
r - a r - b
0................................................................................00
0 b .
. b .
. b .
. a b .
. b .
. a d .
. b d d .
. d d .
. a b X c .
. a a c d .
. a a c .
. c .
. c d .
. c .
. c .
. c 0
00................................................................................0
r - c r - d
r - a,b,c,d - rakety
a,b,c,d - "zhruba" jak by měla vypadat trajektorie jednotlivých raket
P.S.: omluvte mé "malířské schopnosti"
Offline
#2 11. 04. 2009 09:30
Re: Rada - zajímavá úloha
tohle je velice zajímavá úloha:) ale opravdu mě nenapadá jak vypočítat trajektorii, asi jen že to bude spirála vycházející z rohů a končící v průsečíku úhlopříček.
PS: tvé malířské schopnosti jsou úctyhodné, protože dokázat tohle jen s pismenky a mezeramy asi nebylo jednoduché
R. P. Feynman:Fyzika je jako sex, může přinést praktické výsledky, ale to není důvod, proč to děláme.
Offline
#3 11. 04. 2009 10:07
Re: Rada - zajímavá úloha
↑ allergo:Ja by som to asi riešil tak ako ty: proste by som si kreslil. Pre presnejší výsledok by som nechal počítač, aby kreslil za mňa. Zaznamenával by som polohy rakiet po nejakých krátkych časových okamžikoch. Pričom na každom úseku by sa raketa pohybovala priamočiaro smerom k polohe rakety na začiatku toho krátkeho intervalu. V ďalšom intervale by trochu zmenila smer pohybu.
Ale rád by som videl aj nejaké analitické riešenie, len nad tým sa teraz veľmi nestíham zamýšľať.
You know who
(or maybe not)
Offline
#4 11. 04. 2009 10:08 — Editoval kaja.marik (11. 04. 2009 10:11)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Rada - zajímavá úloha
zkuste hledat pojmy jako "krivka pronasledovani" nebo pursuit curve. vede to na diferencialni rovnici. Je to trosku podobne jako krivka tahnuti na http://user.mendelu.cz/marik/videa/video-trac.pdf
myslim ze analyticke reseni bude dost komplikovane, v literature se vetsinou pracuje s faktem ze pronasledovany objekt se pohybuje po primce nebo nejake jednoduche krivce.
moyna pomuze kniha skrasek-tichy Základy aplikované matematiky, ale nevim ktery dil, ani ji nemam k dispozici. Jenom si vzpominam ze jsem tam neco vic nez pronasledovani po primce behem studi videl.
-------
Dávno, dávno jž tomu ........
Offline
#5 30. 04. 2009 21:59 — Editoval kaja(z_hajovny) (30. 04. 2009 21:59)
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: Rada - zajímavá úloha
↑ kaja.marik:
ja bych jeste k prispevku sveho krajana doplnil, ze numericke reseni v sage je na http://wiki.sagemath.org/interact/graph … sofPursuit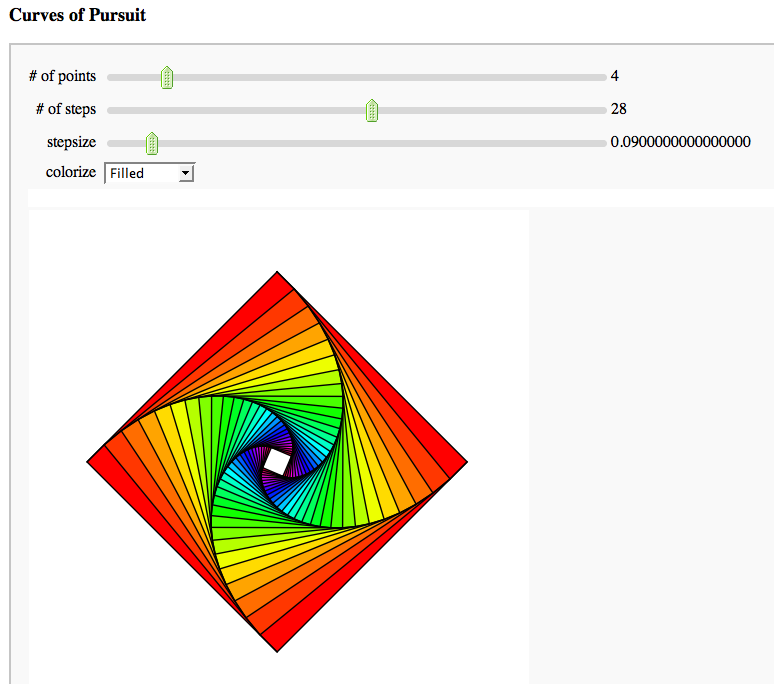
Offline
#6 01. 09. 2009 21:19
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Rada - zajímavá úloha
Jen doplňuji, že se v řešení této úlohy pokračuje v tomto tématu.
Offline
#8 02. 09. 2009 09:57 — Editoval BrozekP (02. 09. 2009 12:50)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Rada - zajímavá úloha
↑ Cheop:
Chápu tedy správně, že  značíš stranu n-úhelníku,
značíš stranu n-úhelníku,  rychlost rakety,
rychlost rakety,  je doba, za kterou se rakety srazí, a
je doba, za kterou se rakety srazí, a  je při tom uražená dráha rakety? Já jsem došel k jinému výsledku:
je při tom uražená dráha rakety? Já jsem došel k jinému výsledku: EDIT: můj výsledek není dobře.
EDIT: můj výsledek není dobře.
Pro  to vyjde stejně, ale obecně se to liší. Jakou cestou jsi ke svým výsledkům došel? Já jsem postupoval jako v tomto tématu.
to vyjde stejně, ale obecně se to liší. Jakou cestou jsi ke svým výsledkům došel? Já jsem postupoval jako v tomto tématu.
Offline
#9 02. 09. 2009 10:24
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Rada - zajímavá úloha
↑ BrozekP:
Já to počítal takto (možná chybně)
http://forum.matweb.cz/upload/1251879832-Rakety.JPG
Nikdo není dokonalý
Offline
#10 02. 09. 2009 12:49
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Rada - zajímavá úloha
↑ Cheop:
Máš to správně, měl jsem u sebe chybu.
Offline



