Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 17. 01. 2008 16:23
Re: Nekonečno ála nekonečno
↑↑ robert.marik:
Tomu neverim. Muzete to nejak vice rozvest a presvedcit me?
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#27 17. 01. 2008 17:30
Re: Nekonečno ála nekonečno
↑ Lishaak:
Jednou se mi snazil neco takoveho vysvetlit jeden znamy, bylo to neco ve smyslu, ze napr. kdyby se vybiralo z nekonecneho mnozstvi prvku, tak jaka byla sance, ze sis vybral prave ten jeden prvek, ktery sis vybral? 0 . Neco takoveho podle mne robert myslel
Offline
#28 17. 01. 2008 18:22
Re: Nekonečno ála nekonečno
Když už jsme u těch nekonečných množin a pravděpodobností, docela zajímavým faktem je, že pravděpodobnost, že dvě náhodně zvolená celá čísla jsou nesoudělná, je rovna 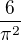 .
.
Offline
#29 17. 01. 2008 18:24
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Nekonečno ála nekonečno
zkusim najit nejaky odkaz. U klasicke pravdepodobnosti to pochopitelne nenastane, ale jsou i jine druhy pravdepodobnosti, napriklad geometricka. Jestli najdu vhodny odkaz, dam ho sem. Ale urcite to bude dost prekracovat uroven SŠ. Anebo sem napise jak to je nekdo, kdo ma vetsi prehled (Kondr, Marian, Jelena ....) a nema zrovna dite pod nohama :)
Offline
#30 17. 01. 2008 20:30
Re: Nekonečno ála nekonečno
↑ Lishaak:
Tak sa rozbehla mila debata :) Lishaak, jasne, ze na nicom nestaviam :) Ja sa pytam Teba. A rad by som tomu pochopil, tak skus vysvetlit, preco je pravdepodobnost nulova. Priklad od Hoba sa mi paci, vystihuje to moje myslienky :) (DIKY). Ale nechapem, matematika je predsa o presnosti, stavia len na faktoch, teda na pravdivych a presnych definiciach. Robime len to, co robit vieme. A predsa niekto tvrdi, ze nieco s nulovou pravdepodobnostou moze nastat? Potom je asi rec o inej nule, nez tej klasickej, o ktorej hovorime, ze?
Offline
#31 17. 01. 2008 21:09
Re: Nekonečno ála nekonečno
↑ robert.marik:
Pokud ten odkaz najdete budu jen rad. Pokud to bude prekracovat uroven SŠ jen dobre. Za tyden delam zkousku z VS pravdepodobnosti a statistiky :-)
↑ xificurC:
Zkusim to rict jeste jinak. Vsechny matematicke teorie jsou vybudovane na zakladni sade predpokladu, kterym se rika axiomy (napr. na kazde primce lezi aspon dva body apod.). Takova teorie se buduje exaktne a vyvozuje se jenom z tech axiomu naprosto nezavisle na tom, co je pravda v okolnim svete. Takovato teorie nemusi mit s nasi realitou nic spolecneho (existuje treba druh logiky (rika se ji dvousortova modalni logika), ve ktere se da matematicky dokazat, ze existuje Buh). Takova logika nema s nasim svetem nic spolecneho. Jine teorie muzou mit s nasim svetem spolecneho jenom neco.
Matematicke teorie, kterou pouzivame bezne my je zatim nejlepsi aproximace realneho sveta. Rikam zatim, protoze se muze objevit nekdo (jednou se takhle objevil jeden clovek, ktery se jmenoval Einstein), ktery ukaze, ze jina teorie tento svet popisuje lepe.
Mame tedy teorii pravdepodobnosti a ta nam rika, ze realne cislo nejde uhodnout. Tohle je poznatek z teorie a zatim neni duvod se domnivat, ze to v realnem svete neplati. Za deset let ale treba prijde nekdo, kdo udela takovy experiment (v nejdivocejsi fantazii si nedokazu predstavit jaky), ktery prokaze, ze to v realnem svete neplati. Potom budeme muset vzit jinou teorii pravdepodobnosti, ktere bude lepe korespondovat s realnym svetem (stejne jako Einstein ukazal fyzikum, ze je treba vzdat se euklidovske geometrie a pouzit jinou, ktera tento vesmir popisuje lepe).
Pokud chces vedet, jak ta nulova pravdepodobnost plyne z teorie, tak nevim jak to rict nejak jednoduse. Napadaji me dva mozne zpusoby. Jeden vychazejici z geometricke pravdepodobnosti a druhy, pracujici s pojmem hustota pravdepodobnosti. Oba se ale dost opiraji o teorii miry a nevim cemu z toho bys lip rozumel a co by te vic presvedcilo.
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#32 24. 01. 2008 11:39
Re: Nekonečno ála nekonečno
↑ Lishaak:
Ani ja neviem, kedze neviem, co je teoria miery :) Ale velmi rad si to vypocujem :)
Teda otazocka este: hovorime, ze trojdimenzionalny priestor sa sklada z nekonecne vela dvojdimenzionalnych?? Neviem si to presne predstavit, lebo ked ano tak potom ani dvojdimenzionalny priestor by nemohol mat hrubku 0 (absolutna nula), lebo by z ich zlozenia bol stale len dvojdimenzionalny priestor. A ked nie, z coho sa potom sklada trojdimenzionalny priestor? :)
Offline
#33 24. 01. 2008 12:33
Re: Nekonečno ála nekonečno
Kdo tvrdi, ze soucet nekonecne mnoha nul je nula?
Co se tyce te geometricke pravdepodobnosti:
Primka ma miru nekonecno, bod ma miru 0. 0/oo = 0. Tedy neni sance ten bod trefit.
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#34 24. 01. 2008 13:17
Re: Nekonečno ála nekonečno
Ja tvrdim :D Ale nie, ked hovorime o niecom, co sa blizi k nule, v poriadku, vtedy je to neurcite. Ale pri absolutnej nule som sa ucil (aj na vyske), ze hocico krat nula je nula, aj nekonecno... Ak sa v niecom mylim, oprav ma, budem len rad, ked to pochopim ;)
K pravdepodobnostnej teorii: Ty hovoris o 0/oo , no predtym sme sa bavili o 1/oo...
Offline
#35 24. 01. 2008 14:31
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Nekonečno ála nekonečno
V okamžiku kdy se bavíme o něčem tak neuchopitelném jako je nekonečno musíme opustit intuici a ponořit se do teorie. Z ní vyčteme například že:
* Nekonečna jsou různá. Nejmenší nekonečno je spočetné (počet přirozených čísel), další jsou nespočetná (počet reálných čísel)
* Spočetně mnoho bodů má míru nula. Proto šance, že jeha hozená na číselnou osu se zabodne do přirozeného čísla je 0/oo=0. Spočetně mnoho rovin nikdy nevytvoří celý prostor.
* Interval (0,1) má míru 1. Šance že se do něj tou jehlou trefíme je 1/oo=0.
Sám nemám dost nastuované teorie, abych o tom mohl nějak zasvěceně psát. Věřím ale, že na internetu se zdroje najdou.
A k tomu oo krát 0: v reálných číslech žádné oo není, takže 0.oo v nich nemá význam. Definuje se i množina R*, která krom prvků R obsahuje oo a -oo. Pokud vím, tak prvky R i R* jsou definovány jako limity posloupností prvků Q, takže násobením zase vyjde limita nějaké posloupnosti zlomků, což je neurčitý výraz.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#36 24. 01. 2008 14:36
Re: Nekonečno ála nekonečno
To je jedno. Miru jedna ma treba interval (0, 1). Takze muzeme se ptat, jaka je pravdepodobnost, ze tazene realne cislo bude z intervalu (0, 1)? Je to nula.
Ted se treba muzem ptat, jaka je pravdepodobnost, ze tazene realne cislo bude z intervalu (-x, x), kde x je pocet vsech atomu ve vesmiru (ted predpokladam ze vesmir je konecny, snad je to pravda, nejsem fyzik). Bude to zase nula (podle geometricke pradepodobnosti, kdyz se nad tim zamyslim z hlediska hustoty pravdepodobnosti, tak uz trochu ztracim pevnou pudu pod nohama, chtelo by to nekoho, kdo v tom ma vetsi zkusenosti).
Pokud si myslis, ze soucet nekonecne mnoha nul je nula, tak to dokaz. Ja osobne si myslim, ze to nula neni. To by se mohlo dokazat nejak sporem, az budu mit cas, treba o tom zkusim neco pohledat.
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#37 24. 01. 2008 14:44 — Editoval Marian (24. 01. 2008 14:44)
Re: Nekonečno ála nekonečno
↑ Olin:
To co Olin pise, je skutecne jeden zajimavy fakt z teorie cisel. Jeho dukaz sice neni elementarni, ale chtel jsem se jen zminit, ze cela tato tematika je nazvana souhrnne jako
"points visible from the origin".
Informace najdete treba zde. Hezke pojednani i s dukazem o techto vecech je napriklad ve vynikajici knize
Apostol, T. Intorduction to the Number Theory.
Dokonce se da tato kniha stahnout z internetu. Pokud by byl zajem, dam zde odkaz.
Offline
#38 24. 01. 2008 15:36
Re: Nekonečno ála nekonečno
↑ Lishaak:
Co mam dokazat, ze oo * 0 = 0? Nepochopil som otazke, lebo to mi pripada na indukciu (len neviem, ci je pri nekonecnu nieco take pouzitelne). Kedze 0 + 0 = 2 * 0 = 0 atd a pre k+1 to bude platit tiez, pre k patriace N...
Offline
#39 24. 01. 2008 15:51
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Nekonečno ála nekonečno
Indukce by se dala použít, pokud bychom chtěli ukázat, že každé přirozené číslo krát nula je nula. Nekonečno není přirozené číslo.
Navíc: nekonečno krát nula si NEJDE představit jako 0+0+0.... do nekonečna. To by šlo jen za předpokladu, že by to nekonečno, kterým násobíme, bylo spočetné (pak by ten součet opravdu vyšel nula, např. ze vzorce pro součet nekonečné geometrické řady s kvocientem 1/2).
Doporučuji najít na internetu či v knihovně něco o teorii míry, teorii množin a geometrické pravděpodobnosti. Diskuse založená na intuitivních představách se může zdát zábavná, ale je ztrátou času.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#41 05. 10. 2016 03:10
Re: Nekonečno ála nekonečno
↑↑ Lishaak: To co píšeš je nesmysl. Řekl bych že je to tak, jak píše robert.marik, že statistika zná jev nemožný který má vždycky pravděpodobnost nula, ale né každý jev který má pravděpodobnost nula je nemožný. To, že tvé tvrzení, že možnost že padne dané číslo je nemožné se dá snadno vyvrátit. Pokuď totiž budeš tvrdit že to číslo nemůže padnout, mohl by jsi to tvrdit o kterémkoli jednotlivém čísle z nekonečna, nakonec by ti nezbylo žádné číslo, které by mohlo. Ale něco padnout musí a může to být cokoli, takže je stěží nemožné, aby to nějaké číslo bylo. V tomhle případě je naopak logické předpokládat, že jakékoli číslo je možné a ty bys měl dokázat, proč by bylo nemožné. V zásadě je třeba brát všechno presumpčně jako možné než to vyloučíš. V čisté statistice nemůže být nic nemožné Nemožnost musí vycházet z kauzality nebo definice na začátku, když ale na začátku situaci definuješ tak, že máš nekonečno čísel a může padnout kterékoli z nich tak taky každé padnout může. Argumentoval si tím, že za tvojí úvahou byla teorie, ovšem špatně použitá (a defacto založená jen na definici a axiómu, který jsi možná špatně pochopil a hlavně nekriticky podsouval) zatímco xificurC nepoužil žádný argument ale jeho předpoklad neodporuje základní logice.
Offline
#42 05. 10. 2016 04:01
Re: Nekonečno ála nekonečno
Fyzicky by se to dalo dokázat jednoduše, kdyby hádal nekonečný počet hádajících rovný počtu čísel a každý jiné číslo, pak by jeden uhodnout musel. Samozřejmě reálně nemůžeme udělat nekonečný počet hádajících ani stroj, který by číslo generoval. To jestli té pravděpodobnosti budete říkat nula nebo 1/oo je celkem jedno, ale určitě to není nemožné ani stejná nula jako nemožné. Navíc my zní jako nesmysl, předpokládat, že 1/oo je nula a zároveň že 0 x oo je nula. když 1/oo = 0 pak 1=0 x oo v tomhle případě jde o nekončno které z 0 udělá jedničku ale mohlo by být i jiné, protože pak by platilo i že 5/oo = 0, protože 5x0 je pořád 0, jenže nekonečno by tu bylo jinak definované, řekněme, že nekonečno bychom používali jako znak, který sice vždy značí nekonečno nicméně by se lišilo nějaký indexem, který bychom připisovali. Omlouvám se, nejsem matematik, takže nevím jak to je ale tohle mi přijde logické. Nicméně by pak platilo i že 0 x oo = 5 atd. pak by oo bylo pořád jinak definované. Takže když tvrdíte že 1/oo je 0, logicky tedy 0 x oo může být cokoli podle toho, jak oo nadefinujete, jediné, čím si nejsem jist, jestli to může být zase nula. V našem případě ale pracujeme jenom s nekonečnem které je definované tak že 0 x oo = 0 (nevím jestli včetně) až 1, protože pravděpodobnost definujeme jako od 0 do 1. Definuji to tak proto, že můžu vybrat třeba všechna sudá čísla, kterých bude polovina (kromě nuly) přitom se ale pravděpodobnost, že něco z toho padne skládá ze samých nulových pravděpodobností, z nekonečna nulových pravděpodobností, v tomto případě tak nuly složili jednu polovinu, klidně bychom tohle nekonečno mohli definovat jako nekonečno poloviční, s tím, že jako celé nekonečno bychom definovali nekonečno potřebné ke složení všech čísel a jisté pravděpodobnosti 1. Takhle bych si přál pracovat s nekonečnem, v zásadě by stačilo určit počáteční bod, co je základní nekonečno a co je nekonečno různě poměrné. Člověk nemusí mít problém pracovat v rovnici s nekonečnem, většinu času mu stačí fakt, že daná hodnota je nekonečno, tahle informace je to hlavní v té chvíli, ve chvíli, kdy to nestačí, se dá k nekonečnu psát jaké. Nekonečno podrží část informace z jiné části rovnice.
Offline