Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Velikost vektorového úhlu (TOTO TÉMA JE VYŘEŠENÉ)
#1 12. 09. 2009 13:34
Velikost vektorového úhlu
Jsem 20 let ze školy, tak se, prosím, nelekejte :
Dle vašich instrukcí (jiných tazatelů) jsem vypočítala skalární součiny a délky vektorů. Dál mám vypočítat velikost jejich úhlů. Našla jsem vzoreček cos (konvex. úhlu) = skal. součin/vel. vektoru. Výsledek mi u všech 3 vektorů vyšel 1.
Ale co to je: cos (konvex.úhlu)=1. Je to pravý úhel? nebo kolik je to stupňů? Jak to zjistit? Potřebuji totiž dále zjistit, zda vektory tvoří ortonormální bázi.
Děkuji předem za polopatickou odpověď.
Offline
#2 12. 09. 2009 14:01 — Editoval LukasM (12. 09. 2009 14:30)
Re: Velikost vektorového úhlu
↑ Maca:
Ahoj. Pokud ti vyšel cos nějakého úhlu jedna, znamená to, že je to nějaký celočíselný násobek 2pi (tedy 360ti stupňů). Plyne to ze základních vlastností funkce cos - podívej se na graf nebo jednotkovou kružnici.
Nicméně na tom zbytku se mi něco stejně nezdá. Ten vzoreček pro cos konvexního úhlu dvou vektorů by měl být  ( x,y - vektory, (x,y) jejich sk. součin, ||x|| je délka x ). Ve jmenovateli jsi nejspíš zapomněla napsat délku toho druhého vektoru.
( x,y - vektory, (x,y) jejich sk. součin, ||x|| je délka x ). Ve jmenovateli jsi nejspíš zapomněla napsat délku toho druhého vektoru.
Pokud to ale děláš kvůli zjišťování ortogonality, pak stačí spočítat jenom ten skalární součin - dva vektory jsou kolmé, když je jejich skalární součin nula. Když pak zjistíš, že ta báze je ortogonální, stačí vektory vydělit jejich délkou a je z ní ortonormální.
Jinak sem zkus napsat celé zadání toho příkladu, ať se určitě bavíme o tom samém. A když napíšeš rovnou i svůj postup, tak se taky nic nestane :-)
Snad jsem nic nespletl.
Edit: Trochu jsem to prve pomotal s tou absolutní hodnotou. Pro výpočet úhlu vektorů ve vzorci není, objeví se tam až při výpočtu úhlu přímek, kdy chceme úhel menší než 90 stupňů. Opravil jsem to, ale v našem případě to moc nemění.
Offline
#3 12. 09. 2009 14:36
Re: Velikost vektorového úhlu
↑ LukasM:
Asi nezvládnu přepis znaků... takže druhou odmocninu ze 2 to celé lomeno dvěma zapíši (2)/2 ... druhou odmocninu z 1 zapíši sqr (1)..... OK?
Zde je příklad: Jsou dány vektory: a=(2)/2 (1,0,1) b= (0,1,0) c=(2)/2 (-1,0,1). Určete velikost těchto vektorů a úhly, které spolu svírají. Rozhodněte, zda tvoří ortogonální či ortonormální bázi prostoru E3.
Můj pokus o řešení:
K výpočtu velikosti vektoru potřebuji znát skalární součin.
skalární součin a = (1*(2)2/2) * (1*(2)/2) + (0*(2)/2) * (0*(2)/2) + (1*((2)/2) * (1*(2)/2) = (1*2/4)+0+(1*2/4)=1/2+0+1/2=1
velikost vektoru a = lal = sqr (1) = 1
Dále jsem se dočetla, že velikost úhlu se vypočítá: cos konvex. úhlu= skal. součin/ velikost vektoru. Z toho :
cos KÚ=1/1=1
Tímto postupem mi pak u všech vektorů vyšla velikost úhlu =1. Jsem hodně mimo?
Offline
#4 12. 09. 2009 14:55 — Editoval kaja(z_hajovny) (12. 09. 2009 14:57)
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: Velikost vektorového úhlu
↑ Maca:
Je-li uhel mezi dvema vektory  a
a  roven
roven  , platí
, platí  kde <.,.> je skalární součin a ||.|| norma (délka)
kde <.,.> je skalární součin a ||.|| norma (délka)
takže třeba úhel mezi vektory  a
a  je devadesát stupňů, protože skalární součin je nula a kosinus devadesáti stupňů je taky nula.
je devadesát stupňů, protože skalární součin je nula a kosinus devadesáti stupňů je taky nula.
Všechny vektory mají délku jedna, každé dva jsou kolmé a navíc je jich správný počet (tři), takže tvoří ortonormální bázi
Offline
#6 12. 09. 2009 15:10 — Editoval LukasM (12. 09. 2009 15:13)
Re: Velikost vektorového úhlu
↑ Maca:
No, zas tak úplně mimo nejsi, ale dosazuješ do toho vzorečku pro úhel špatná čísla. To že skalární součin  je pravda, když to odmocníš, opravdu dostaneš velikost toho vektoru a. Až sem je to v pořádku.
je pravda, když to odmocníš, opravdu dostaneš velikost toho vektoru a. Až sem je to v pořádku.
Pokud ale počítáš úhel dvou nějakých vektorů, musíš (kvůli tomu vzorečku) spočítat skalární úhel TĚCH DVOU vektorů, tedy třeba 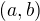 . Když bys použila vzoreček
. Když bys použila vzoreček  (cos udělala), vyjde ti vlastně kosinus úhlu, který ten vektor svírá sám se sebou - proto ti vyšla jednička a úhel vektorů tedy 0 stupňů (logicky). Vlastně je to logické - vypočítat úhel dvou vektorů když do výpočtu použiješ jen jeden z nich je nesmysl.
(cos udělala), vyjde ti vlastně kosinus úhlu, který ten vektor svírá sám se sebou - proto ti vyšla jednička a úhel vektorů tedy 0 stupňů (logicky). Vlastně je to logické - vypočítat úhel dvou vektorů když do výpočtu použiješ jen jeden z nich je nesmysl.
Je to jasné?
Edit: doplnění - zkrátka a jasně, skalární součin je vždy něčeho s něčím - a je potřeba si uvědomit čeho s čím zrovna potřebuju.
Offline
#7 12. 09. 2009 15:54
Re: Velikost vektorového úhlu
Dobře, pak tedy:
u (a,b)=((2)/2,0,(2)/2) * (0,1,0) / 1*1 = 0+0+0 / 1 = 0 cos 90 st = 0
u (b,c)= 0
u (a,c)= 0
A už se dostávám k větě od Káji, že jsou vektory kolmé, jsou 3 a mají délku 1, takže tvoří ortonormální bázi. :)
Jste skvělí, moooc děkuji a ještě se ozvu.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Velikost vektorového úhlu (TOTO TÉMA JE VYŘEŠENÉ)
