Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 11. 2009 18:05
Aritmetická posloupnost ......
Mam takový problém s příkladem:
V aritmetické posloupnosti určete sučet prvních osmi členů, jestliže platí:


difference mi vyšla -3 a a_1 5 , ale jak mam ted zjistit součet prvních 8 členů? podle vzorce S_n jsem to dělal, ale nějak to nevychází, nebo nevim jak S_8 mi vychází =52-12_n a co s tim ted? Děkuji za odpověď........ jo a má to vyjít 28,, ale potřeboval bych zjistit jak na to....
Offline
#2 11. 11. 2009 18:16 — Editoval septolet (11. 11. 2009 18:19)
Re: Aritmetická posloupnost ......
Součet prvních n členů se spočítá podle vzorce: S_n = n/2 * (a_1 + a_n). Kde n je počet členů, a_1 je hodnota prvního členu, a_n je hodnota posledního členu. Pokud tedy máš a_1 a d stačí dosadit do vzorce (a_n můžeš vyjádřit pomocí a_1 a d).
Offline
#3 11. 11. 2009 18:21
Re: Aritmetická posloupnost ......
↑ septolet: když si vyjádřim a_n tak to mi výjde a_n=8-3n a když to dám potom do vzorce , tak mi to výjde S_8= 52 - 12_n .
Offline
#5 11. 11. 2009 18:35 — Editoval septolet (11. 11. 2009 18:40)
Re: Aritmetická posloupnost ......
Ano, to máš dobře spočítané. Diference vyjde -3, a_1 = 5 a a_n = 8 - 3n. Teď to dosaď do toho vzorce pro součet prvních n členů jak jsem psal o kousek výše.
EDIT: Součet prvních 8 členů skutečně vyjde -44, jak si už psal. Řekl bych tedy, že si to spočítal správně.
Offline
#6 11. 11. 2009 18:42 — Editoval tob (11. 11. 2009 18:43)
Re: Aritmetická posloupnost ......
↑ septolet: no to jsem právě udělal, ale vyšlo mi 
ale ve výsledku vyjde 28
Offline
#8 11. 11. 2009 18:49
Re: Aritmetická posloupnost ......
↑ septolet:
jj už mi to taky vychází -44 , ale nechápu, proč ve výsledkách v knížce píšou, že to výjde 28 ....
Offline
#12 11. 11. 2009 19:08 — Editoval septolet (11. 11. 2009 19:09)
Re: Aritmetická posloupnost ......
Opět budeme dosazovat do vrozečku uvedeném v mém prvním příspěvku v tomto vlákně.
a) První přirozené číslo je 1 (a_1), poslední (200.) je 200 (a_200), dosaď to do toho vzorečku (n = 200) a vyjde 20100.
b) Lichých čísel menších než 100 je 50 (n). Je to každé druhé číslo. První liché je 1 (a_1), poslední liché menší než 100 je 99(a_50). Opět dosadíš do toho vzorečku a vyjde 2500.
Offline
#16 11. 11. 2009 20:31
Re: Aritmetická posloupnost ......
↑ tob:
Dosadíš do předpisu a dostaneš:
Předpis
První člen


a) 
Zjistíme, zda je posloupnost aritmetická - vypočteme ještě třetí člen


Je to posloupnost aritmetická s diferenci 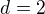
Teď už můžeme určit i případy b), c), d)
b)  rozdíl dvou následujících členů je difrence d
rozdíl dvou následujících členů je difrence d
c) 
d) 
Offline
#17 11. 11. 2009 20:57
Re: Aritmetická posloupnost ......
Děkuji chrpa
Ještě tu mam příklady.... ( to je poslední co chci, zejtra píšem pís. a já se to doučuju :) a mam tu hafo příkladů.....) (všem co mi odpoví děkuju)
Určete první čtyři členy aritmetické posloupnosti, je-li dáno:

a
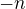 (n na druhou, lomeno čtyřma , to celé -n )
(n na druhou, lomeno čtyřma , to celé -n )
a
Ulohu
Dělník vyrobí za směnu 45 součástek.
Kolik součástek by vyrobil za 20 směn, kdyby svůj výkon postupně zvyšoval každou směnu
o 2 součástky?
Offline
#18 11. 11. 2009 21:07
Re: Aritmetická posloupnost ......
K té slovní úloze:
45 je výchozí stav, první člen posloupnosti, čili a_1.
S každou směnou vyrobí o 2 součástky více, čili diference d = 2.
Chceš vědět, kolik součástek vyrobí dohromady za 20 směn, když každou směnu vyrobí o 2 součástky více, čili použiješ opět vzoreček pro soušet prvních n členů, n je v tomto případě 20. Všechno potřebné máš, tak to zkus vypočítat. Kdyby ses někde zasekl, tak dej vědět.
Offline
#19 11. 11. 2009 21:13 — Editoval Chrpa (12. 11. 2009 10:33)
Re: Aritmetická posloupnost ......
↑ tob:
Př.2)
Pro aritmetickou řadu platí: (tento příklad je aritmetická posloupnost, protože každou směnu vyrobí dělník o 2 součástky víc než směnu předcházející)
diference posloupnosti je tedy 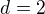
Pro aritmetickou řadu platí: - n-tý člen řady
- n-tý člen řady součet prvých n- členů aritmetické řady.
součet prvých n- členů aritmetické řady.
Pro náš případ:
První člen
Offline
#21 11. 11. 2009 21:22 — Editoval septolet (11. 11. 2009 21:25)
Re: Aritmetická posloupnost ......

Pokud postupně dosadíme 1, 2, 3, 4 dostaneme po řadě čísla 3, 8, 15, 24. Víme že to je aritmetická posloupnost, takže ke každému předcházejícímu číslu přičteme stejné číslo (diferenci) a dostaneme číslo následující. Součet prvního členu je 3, čili a_1 = 3. Dále platí: a_2 = a_1 + d. Pro součet prvních dvou členů platí, že je roven 8, přičemž první člen je 3, z toho je jasné, že a_2 = 5 a d = 2.
První 4 členy jsou tedy: 3, 5, 7, 9
Offline
#25 12. 11. 2009 09:09
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Aritmetická posloupnost ......
↑ tob:
Úplně jednoduše
Př. 1)
nevím co ten ↑ Chrpa: vymýšlel.
1a)
Předpis:


Diference řady je: 
První 4 členy poslloupnosti jsou:
1b)
Předpis


Diference řady je: 
První 4 členy poslloupnosti jsou:
A je hotovo.
Nikdo není dokonalý
Offline




 což je zjevně nesmysl. Nebo jsem Tvůj zápis příkladu špatně pochopil.
což je zjevně nesmysl. Nebo jsem Tvůj zápis příkladu špatně pochopil.
 tj:
tj:




