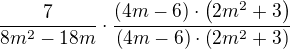Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#251 18. 11. 2009 06:45
- robo.n.x12
- Zelenáč
- Příspěvky: 8
- Reputace: 0
Re: Lomené výrazy
↑↑ Honza Matika:
zádání je nápsáno správně....už se mi párkrát stalo že se přepsali ve výsledcích a já si pak myslel že jsem počítal špatně....i tak vám velice děkuji
Offline
#253 29. 11. 2009 15:37
#254 29. 11. 2009 15:49
Re: Lomené výrazy
přepis: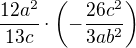
výpočet:
nejprve jsem si upravil jednotlivé hodnoty tak, aby bylo jasné, co se bude krátit (nepovinný krok), pak - protože násobení dvou zlomků můžeme napsat jako násobení jejich čitatelů v čitateli a jmenovatelů ve jmenovateli společného zlomku. A do třetice jsem vše pokrátil:![kopírovat do textarea $\frac{4a\cdot 3a}{13c} \cdot \frac{\(-1\) \cdot 2c \cdot 13c}{3a \cdot b^2} =\nl \frac{\(4a \cdot 3a\) \cdot \[\(-2c\) \cdot 13c\]}{\(13c\) \cdot \(3a \cdot b^2\)} =$](/mathtex/bf/bfe598326d58498e65d476a2efc36433.gif)
zbavím se závorek a pokrátím:
Offline
#255 29. 11. 2009 15:49 — Editoval Honza Matika (29. 11. 2009 15:50)
#256 29. 11. 2009 16:13
Re: Lomené výrazy
↑ Honza Matika:
hold je rychlejší :-)
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#257 04. 12. 2009 23:14
#258 04. 12. 2009 23:18
Re: Lomené výrazy
↑ TOMASKO: ...
pošli nějaký příklad na kterém se můžeš učit postupy k řešení.
Jinak základem je znalost sčítání a odčítání jednoduchých zlomků .
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#259 04. 12. 2009 23:19
#260 04. 12. 2009 23:25
#261 04. 12. 2009 23:26
Re: Lomené výrazy
↑ TOMASKO:...
levou myší kopírovat a potom sem vložit a nebo napsat příklad tak, jak to zvládneš :-)
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#262 04. 12. 2009 23:36
#263 04. 12. 2009 23:45 — Editoval Doxxik (05. 12. 2009 00:08)
Re: Lomené výrazy
předpokládám, že přepis bude: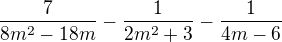 (doufám, že jsem ty dvoky za "m" dal správně do exponentu..
(doufám, že jsem ty dvoky za "m" dal správně do exponentu..
edit: návod na řešení:
co potřebuješ udělat, aby bylo možné tyto zlomky odečíst (resp. sečíst)?
jak to uděláš?
jak to tedy bude u tvého příkladu?
*)
Offline
#264 04. 12. 2009 23:48
#265 04. 12. 2009 23:55 — Editoval Honza Matika (05. 12. 2009 00:09)
#266 04. 12. 2009 23:59
Re: Lomené výrazy
↑ Honza Matika:
Nemalo výsledok by mal byť 3-m
......................
m(2m+3)(2m-3)
výsledky sú ale niekedy zle
Offline
#267 05. 12. 2009 00:08
#268 05. 12. 2009 00:10
#269 05. 12. 2009 00:17
#270 05. 12. 2009 00:17
#271 05. 12. 2009 00:27
#273 05. 12. 2009 08:15
Re: Lomené výrazy
↑ TOMASKO: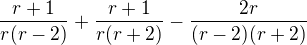
Na společný jmenovatel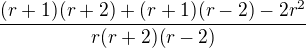
roznásobit závorky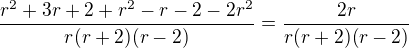
zkrátit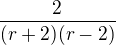
napsat podmínky: 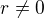 ,
, 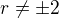
Poznámka: toto je reakce na příspěvek z 0:30, protože tvé příspěvky z 0:27 a 0:30 nejsou stejné. Aby byly stejné, muselo by být v příspěvku z 0:27 ve jmenovateli 3. zlomku 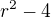 a
a 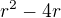
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#274 06. 12. 2009 15:32
Re: Lomené výrazy
ahoj, chcel by som sa opýtať ako upravým lomené výrazy
a+3 a+1
........... - ........... výsledok by mal byť 3(a+1)
a2 -1 a2 +2 .............................. ďakujem, počítal som to :
a(a-1)(a+1)
a+3 a+1 a+3 a+1 a(a+3) - [(a-1)(a+2)] a2 + 3a - [ a2 +a -a -1 ]
............. - ................ = ................ - ........................= ................................... = ......................................... =
a2 - 1 a2 +a (a-1)(a+1) a(a+1) a(a+1)(a-1) a(a+1)(a-1)
a2 + 3a -a2 +1 3a + 1
....................... = ................... kde je ale chyba?
a(a+1)(a-1) a(a+1)(a-1)
..... a ešte by som poprosil jeden lomený výraz : x - 1 4x + 6 3 x - 3
.............. - ................ + ................. výsledok by mal byť ....................
2x + 6 x2 - 9 x - 3 2(x + 3)
počítal som to : x-1 4x +6 3 x -1 4x + 6 3
.............. - ..................... + ................... = ............... - ................... + ............ =
2x + 6 x2 -9 x - 3 2(x + 3) (x-3)(x+3) x-3
(x-3)(x - 1) - [2(4x+6) ] + 6(x+3)
.................................................. = x2 + 2x + 21 - 8x - 12 x2 - 6x + 9
2(x+3)(x-3) .................................... = ..............................
2(x+3)(x-3) 2(x+3)(x-3)
.......... kde ale robím chybu, ďakujem za pomoc.
Offline
#275 06. 12. 2009 15:38 — Editoval Tychi (06. 12. 2009 15:43)
Re: Lomené výrazy
Kromě toho, že ses v prvním příkladu přepsal ([(a-1)(a+2)] místo [(a-1)(a+1)] ) tam chybu nevidím. Pokud by "jejich" výsledek byl správně, tak by ho jistě ještě na konci zkrátili.
ve druhém můžeš ještě čitatele rozložit podle vzorce 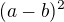 , zkrátit a dojde k hledanému výsledku.
, zkrátit a dojde k hledanému výsledku.
Vesmír má čas.
Offline

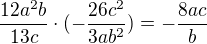

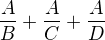 tedy první ze zlomků rozšíříme součinem jmenovatelů 2. a 3. zlomku (tedy o
tedy první ze zlomků rozšíříme součinem jmenovatelů 2. a 3. zlomku (tedy o 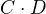 ), druhý součinem jmenovatelů prvního a třetího zlomku (tedy
), druhý součinem jmenovatelů prvního a třetího zlomku (tedy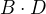 ) a třetí součinem jmenovatelů 1. a 2. zlomku. Dostanu tak:
) a třetí součinem jmenovatelů 1. a 2. zlomku. Dostanu tak: 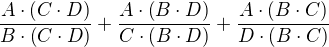 pak se můžeš zbavit závorek (roznásobení závorky; není to ale nutné). Pak stačí vše napsat na jeden zlomek - to proto, že jmenovatele všech jsou stejné (jak je vidět i v příkladě - pořadí členů v násobení totiž nehraje na výsledku roli, a tedy: BCD = CBD = DBC) -> výsledný zlomek bude mít totéž ve jmenovateli (pouze jednou!). V čitateli tohoto zlomku budou čitatele jednotlivých zlomků, které sčítáš/odčítáš/.. s příslušným znaménkem. Pro příklad výše to tedy bude:
pak se můžeš zbavit závorek (roznásobení závorky; není to ale nutné). Pak stačí vše napsat na jeden zlomek - to proto, že jmenovatele všech jsou stejné (jak je vidět i v příkladě - pořadí členů v násobení totiž nehraje na výsledku roli, a tedy: BCD = CBD = DBC) -> výsledný zlomek bude mít totéž ve jmenovateli (pouze jednou!). V čitateli tohoto zlomku budou čitatele jednotlivých zlomků, které sčítáš/odčítáš/.. s příslušným znaménkem. Pro příklad výše to tedy bude: 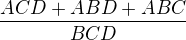
 + další úpravy můžeš provádět dříve, než začneš počítat, aby se nám usnadnilo počítání..
+ další úpravy můžeš provádět dříve, než začneš počítat, aby se nám usnadnilo počítání..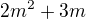 ?
?