Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Spektrální rozklad matice (TOTO TÉMA JE VYŘEŠENÉ)
#1 11. 12. 2009 20:32
- Weithfisto
- Zelenáč
- Příspěvky: 2
- Reputace: 0
Spektrální rozklad matice
Zdravím, mam problem s vyřešením následující matice, matice. Bohužel nevím si stím vůbec rady, mohl by mě někdo napsat doslova bod po bodu jak se tahle úloha má řešit ? Kdyby to bylo s hodmotami z mého přikladu, bylo by to supr. diky
Offline
#2 11. 12. 2009 22:04
Re: Spektrální rozklad matice
↑ Weithfisto:
Ja tomuto prístupu nerozumiem. Do google som dal hľadať "Spektrální rozklad matice" (v českom jazyku) a zhodou okolností ma odkázalo, asi na tvojho cvičiaceho stránky. Odporúčam odkaz
Odkaz
Je tam aj príklad aj čo to spektrálny rozklad je. Čudujem sa, že si o tom nevedel.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#3 11. 12. 2009 22:57
- Weithfisto
- Zelenáč
- Příspěvky: 2
- Reputace: 0
Re: Spektrální rozklad matice
ano o tom vím taky, ale nějak z toho chytrej nejsem :(
Offline
#4 11. 12. 2009 23:34
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: Spektrální rozklad matice
a treba ta vlastni cisla a vlastni vektory se povedlo najit?
Offline
#5 11. 12. 2009 23:57 — Editoval jelena (12. 12. 2009 01:09)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spektrální rozklad matice
↑ kaja(z_hajovny):
Zdravím Vás,
sice jsem měla v plánu, že již nebudu budoucím informatkům ukazovat místní informační středisko, ale když ono nám tak hezky funguje a zde je příběh "Jak jsem se transformovala do androidů", neb jak se vkládá do Wolfram apod.
Měla bych ještě vyhodnotit svou dotazníkovou akci, snad se podaří přes víkend. Mějte se hezky a kolegovi hodně zdaru ve studiu.
EDIT: informační středisko funguje
Offline
#7 12. 12. 2009 13:38
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spektrální rozklad matice
↑ fatality:
x=-1 je dvounásobný kořen polynomu, tedy je to dvounásobné vlastní číslo.
Doporučím ještě tento materiál: od pana Olšáka rozumím dokonce i já (asi každe paté slovo :-) je taková situace rozebrána dost podrobně.
Offline
#9 12. 12. 2009 18:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spektrální rozklad matice
Abych to nějak zrekapitulovala:
a) to je původní matice z projektu, určena k rozkladu.
b) hledáme vlastní čísla a našli jsem jedno dvounásobné (-1) a další 5.
c) zde dosazujeme (-1) místo x (otázka - proč je zde jiný zápis a v 2 řádku je (-1+x) a v 3. řádku (-1+x)), já bych tam čekala stejný zápis jako v prvním řádku).
d) nicmeně, bez ohledu na otázku v bodě c) ve shodě s mou představou vychází matice, kterou používame pro hledání vlastního vektoru.
Jelikož řádky jsou lineárně závislé, po úpravě dostavame matici hodnosti 1, a sice (1, 1, 1). Pro nalezení řešení soustavy: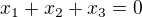 musíme zavest 2 parametry (třeba p, t) a řešení soustavy zapíšeme ve tvaru [p, t, (-p-t)]. Zvolíme parametry p, t tak, abychm nevytvařeli nulový vektor:
musíme zavest 2 parametry (třeba p, t) a řešení soustavy zapíšeme ve tvaru [p, t, (-p-t)]. Zvolíme parametry p, t tak, abychm nevytvařeli nulový vektor:
například p=0, t=1, vektor (0, 1, -1)
například p=1, t=0, vektor (1, 0, -1)
Doufám, že jsem nic nepřehledla a nespletla se ve znamenku. Je to řešení problému, který řešíš nebo máme jiný problém?
----------
.....
Offline
#11 13. 12. 2009 18:12
Re: Spektrální rozklad matice
↑ fatality:
Ahoj. Někdo mně možná opraví, ale nemyslím že je to problém. Jediná neortogonální dvojice je v_2 a v_3, a to jsou vektory příslušející stejnému vlastnímu číslu, které podle mého nemají povinnost být ortogonální.
Jinak to že ty ostatní ortogonální jsou, to taky neplatí obecně, ale jenom u "hezkých" matic (naše matice je symetrická).
Offline
#13 13. 12. 2009 18:55
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spektrální rozklad matice
↑ fatality:
Zdravím přes jiné komunikační prostředky - kolega toto zadání řešil v minulém roce: http://forum.matweb.cz/viewtopic.php?id=1098 tak se nech inspirovat. Ať se podaří.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Spektrální rozklad matice (TOTO TÉMA JE VYŘEŠENÉ)

