Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 10. 12. 2009 13:31 — Editoval Rumburak (10. 12. 2009 13:46)
Re: úprava limity
Předpokládám, že ses chtěl zeptat "Jak upravit tvar funkce funkce pro výpočet limity ?".
Výrez za znakem limity upravíme na 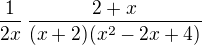 .
.
Po vykrácení dvojčlenem (x + 2) dostáváme funkci spojitou v bodě x = -2 a limitu pak počítáme tímto dosazením .
Offline
#5 12. 12. 2009 09:10
Re: úprava limity
Diky, to uz jsem zkousel, ale ja bych spis potreboval poradit, co u takoveho prikladu pouzit za definici nebo 'vzorecek', protoze z grafu je mi jasne, co to ma vyjit, ale ze bych nasobenim nulami nebo delenim... dostal nekonecno je mi zahadou, abych pravdu rekl. Ted to vemu hypoteticky, kdybych dostal napr. lim x blizici se k nule x na druhou minus 2 lomeno napr. x na druhou, tak at dosadim nulu jak chci, tak nekonecno nebo minus nekonecno nedostanu. Doufam, ze mi rozumite, kde se ztracim.
Offline
#6 12. 12. 2009 21:26
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: úprava limity
↑ Wentworth:
Zdravím, asi neúplně rozumím, v čem je problém: jako příklad uvádiš (pokud jsem dobře luštila):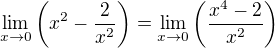
V tomto případě můžeš nulu přímo dosadit, ve výsledku je "číslo/0" (přesně (-2/0)) v limitě dostaneme -oo. Nevím, zda jste již brali jednostranné limity - zde je vhodne kontrolovat, že limita zleva a zprava jsou stejné, proto "-oo" prohlásíme za limitu funkce v bodě 0 (graf vypadá takto)
Pokud při vyšetření limit dosazování hodnoty, ke které se bliží x, do zadání funkce dává ve výsledku "číslo", "číslo/0", "číslo/nekonečno" apod. (ale nedává neurčitý výraz typu "0/0", "oo/oo" apod.) z těchto variant nekonečno dostáváme v situaci "číslo/0" nebo "nekonečno/číslo".
Je problém si představit v limitě "číslo/0" nebo "číslo/nekonečno"? pomůže polopatický výklad?
Doporučuji učebnici Matematika pro gymnazia - Diferenciální počet, případně Limity na mojeskola.cz, v adresové řádce měnit číslo kapitoly, je celkem asi 7.
Případně sem umístí zadání, ve kterých to nevidiš. Ať se vede.
Offline
#7 12. 12. 2009 21:38
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: úprava limity
↑ jelena:
Spíš než nekonečný požitek z jablek (který jsem i jako sadař nějak nepochytil :-)) bych to řekl takto:
Máš limitu 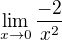 . V nule nevíš, kolik to je, podíváš se tedy mírně vpravo, mírně vlevo. Mírně vpravo (v tomto případě pro x = 1/100) ti vyjde výraz třeba
. V nule nevíš, kolik to je, podíváš se tedy mírně vpravo, mírně vlevo. Mírně vpravo (v tomto případě pro x = 1/100) ti vyjde výraz třeba 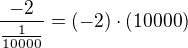 . A čím víc jdeš k nule, tím je to číslo blíž -oo. To samé uděláš i vlevo (vzhledem k tomu, že to je funkce sudá, stačí mrknout jen na jednu stranu).
. A čím víc jdeš k nule, tím je to číslo blíž -oo. To samé uděláš i vlevo (vzhledem k tomu, že to je funkce sudá, stačí mrknout jen na jednu stranu).
Také se to občas nazývá dělení kladnou nulou a něco málo najdeš i po internetech.
Offline
#8 14. 12. 2009 12:53
Re: úprava limity
Dikdy obema, ja uz jsem si to nasel, jsem nemohl prijit na kloub jedne definici a az po vyhledavani jsem nasel Odinuv prispevek tady, ktery to v jedne vete velmi sikovne vysvetlil a vy jste to potvrdili. Ted mam zase jiny problem...a to s priklady tohoto typu...

Nevite o nejakych strankach, kde jsou vsechny vzorecky na tento druh funkci, rovnic a limit... mam tabulky, znam ty zakladni, ale za boha se nemuzu dopracovat ke spravnemu vysledku. Par se mi jich podarilo uspesne dopocitat, ale par jsou fakt humus, v pulce zamotanej, ze bych s tim nejradeji prastil.
Offline
#10 14. 12. 2009 13:04
- marnes

- Příspěvky: 11227
Re: úprava limity
↑ Wentworth:
1. příklad bych rozšířil jmenovatelem s opačným znaménkem mezi dvojčlenem
2. cos 2x bych nahradil cos ^2-sin^2, sin 2x naradil 2 sinxcosx a upravil
Jo. A na začátku vás zdravím.
Offline
#12 14. 12. 2009 13:25
Re: úprava limity
U toho prvniho prikladu po rozsireni je ve jmenovateli nula a v citateli bordel a k tomu nasobek nulou at pocitam jak pocitam. Ja se omlouvam, ze to neprepisuju, protoze nemuzu tu najit jak se to tu pise, takova ta klikajici tabulka se znaky a nemam u sebe kabel na mobil, abych to mohl ofotit.
Offline
#15 14. 12. 2009 13:44 — Editoval Wentworth (14. 12. 2009 13:55)
Re: úprava limity
↑ halogan:
Dekuju, to je to ceho jsem si nevsimnul.
↑ jelena:
Taktez dekuju.
Ja jsem vazne slepej..
Offline
#17 14. 12. 2009 15:18
Offline
#19 14. 12. 2009 15:29 — Editoval Wentworth (14. 12. 2009 15:38)
Re: úprava limity
Muzu mit dotaz, pokud si nechcete zkazit den, tak dal nectete (:, jedna se o tu jednicku, je mozne ji vymenit za cos^2(x) + sin^2(x)? Nemyslim ted v tomto poslednim prikladu, ale kde by se mi to hodilo... Ja jsem v rozpacich v tomhle ted, rovna se to jedna podle vzorce, ale chci se ujistit, ze to je okej. Diky
Offline
#20 14. 12. 2009 15:33 — Editoval zdenek1 (14. 12. 2009 15:34)
Re: úprava limity
↑ Wentworth:
Ano 
Takže kdykoli se ti to hodí
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#22 19. 12. 2009 11:13
Re: úprava limity
Zdravim, pokud se chystate na obed, tak dobrou chut, ti, co se nechystaji zatim, mohli byste mi pomoc s timto prikladem, prosim? Vubec si nevim rady s tim jmenovatelem, byl bych vam vdecny, pokud byste mi ukazali prvni dva kroky, jak na to. Diky
Offline
#24 19. 12. 2009 11:41
Offline


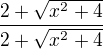 .
. Tak?
Tak?