Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 03. 12. 2009 16:04
Re: Kombinatorika
↑ Tychi: Děkuji za upozornění...
Avšak měl bych ještě jeden dotaz ohledně kombinatoriky...
Měl bych takovéto zadání:
Pro  přirozená čísla dokažte vzorec:
přirozená čísla dokažte vzorec: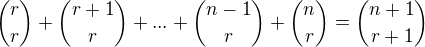
Kombinatorika není zrovna můj "šálek kávy", nicméně šel jsem na to takto:
Definoval jsem si pevné 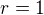 a dal dohromady sumu
a dal dohromady sumu  .
.
Pak jsem se to pokusil ověřit z principu matematické indukce: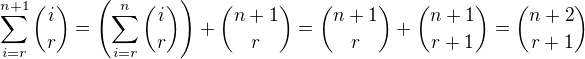
Chtěl bych se vás zeptat, zda je můj postup správný, nebo zda je to naprostá slátanina. Předem děkuji za případnou pomoc.
Offline
#5 03. 12. 2009 23:13 — Editoval petrkovar (16. 12. 2009 08:10)
Re: Kombinatorika
↑ Kein:To, co tu máš vyřešeno, je vlastně indukční krok. Ještě chybí základ indukce: ukázat platnost vztahu pro n=r.
Bonus: existuje i jiný postup. pokud si všimneme, že 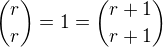 , tak se tvrzení dá dokázat přímo opakovaným užitím kombinatorické identity
, tak se tvrzení dá dokázat přímo opakovaným užitím kombinatorické identity 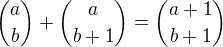 (tato identita se dobře pamatuje tak, že popisuje konstrukci Pascalova trojúhelníka).
(tato identita se dobře pamatuje tak, že popisuje konstrukci Pascalova trojúhelníka).
Offline
#6 03. 12. 2009 23:36
Re: Kombinatorika
↑ petrkovar: Děkuji za reakci :-)
Pokud jsem to pochopil dobře, je tedy můj postup správně - tedy to ověření indukčního předpokladu - pravda ten základ tam napsaný nemám.
add Bonus: S tou kombinatorikou nejsem ještě tak daleko, abych plně dokázal pochopit to znění, nicméně zítra se na to juknu a ještě na tý kombinatorice zapracuju.
Offline
#9 15. 12. 2009 19:12
Re: Kombinatorika
↑ zdenek1: obrázek určitě pomůže... a existuje pro toto i formální definice?
Offline
#12 15. 12. 2009 21:08
Re: Kombinatorika
↑ Kein:
1. Ověříme, že platí pro 
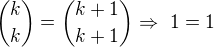 platí
platí
2. předpokládáme, že platí pro 

3. Dokážeme, že platí pro 
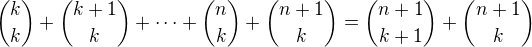 ale to je podle (4)
ale to je podle (4)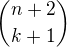 . A to jsme měli dokázat.
. A to jsme měli dokázat.
Když budeš chtít být úplně košer, nejdřív si dokážeš (4).
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#15 18. 12. 2009 01:03
Re: Kombinatorika
↑ zdenek1: Ještě jsem si všimnul, že v tom mém vzorci jsem měl při dokazování špatně proveden součet kombinačních čísel.
↑ petrkovar: Stane se
Každopádně bych vám chtěl ještě jednou poděkovat za pomoc při řešení.
Offline
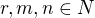 ,
, 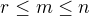 . Dokažte, že platí
. Dokažte, že platí 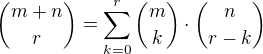
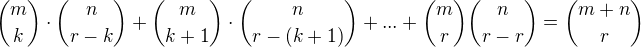

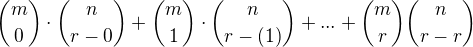

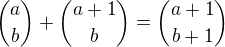 nemělo by toto být spíše
nemělo by toto být spíše 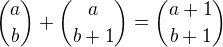
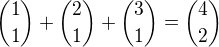 z toho Pascalova trojúhelníku?
z toho Pascalova trojúhelníku?