Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 20. 12. 2009 21:37
Re: help pls
asi bych na to šel tak, že bych si spočítal odchylku zadané přímky od osy x (uprav do tvaru y = kx + q -> k = tg(alfa) -> alfa je ten úhel), pak bych si spočítal, jaké musí být k, aby byl úhel o 45° jiný (získám tedy 2 řešení)
získám tedy rovnici ve tvaru y = k_1 * x + q (kde k_1 známe, q neznáme)
mno a potřebuji zajistit, aby M ležel na dané přímce -> dosadíme jeho souřadnice do rovnice (za x a y) a spočítáme si q
pak opět sepíšeme rovnici + dosadíme za k_1 i za q
y = k_1 * x + q
(nakonec můžeme převést třeba na obecnou rovnici přímky..)
nezapomenout druhé řešení!
Offline
#4 20. 12. 2009 22:21
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: help pls
↑ Doxxik:
Lze také využit vztah pro směrnice jednotlivých přímek, na který se odkazuji v tomto tématu.
V kompletním rozboru řešení pokračujte, prosím, tady. Děkuji.
Offline
#6 20. 12. 2009 22:32
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: help pls
↑ sipsiz:
Tuto přímku ze zadání 4x-2y-1=0 převed na směrnicový tvar, tj. do zápisu y=k_1x+q_1. Odsud zjistiš jedno k_1 do vzorce pro tangens(45 stupňů).
Všechno dosadíš do vzorce a dopočteš k pro druhou přímku: y=k_2+q_2, po dosazení za x, y souřadnic bodu M dopočteš q_2.
Pokračuj, prosím.
Offline
#9 20. 12. 2009 23:03 — Editoval Doxxik (20. 12. 2009 23:12)
Re: help pls
n1 a n2 náleží vzorci, který vyjadřuje odchylku dvou (normálových) vektorů
(níže si za ně dosadil - to první jsou je vektor normálový přímky zadané, to druhé je normálový vektor přímky hledané ..)
edit: pro souřadnice vektoru musí platit, že x a y jsou na sobě závislé (tedy - zvětším-li x, zvětší se mi i y, ...). Zároveň víme, že na velikosti souřadnic vektoru nezáleží (důležité je zachovat mezi nimi charakteristický poměr..).. např vektor s = (12;9) = (4;3) = (8;6) = (40;30) atd..
toho využil kolega výše ↑ zdenek1: a jako y si zvolil hodnotu "1" a pro tuto hodnotu pro souřadnici y hledá příslušnou hodnotu pro souřadnici x, kterou si označil jako "k" -> vypočítáš-li k, máš obě souřadnice daného vektoru..)
Offline
#11 20. 12. 2009 23:14
Re: help pls
"káčka" jsou x hodnoty normálového vektoru hledané přímky. Dosadíš jej (nejprv k1, pak k2 v druhém řešení) do obecné rovnice přímky (ax + by + c = 0; a = k, b = 1), následně dosadíš bod náležící dané přímce (M) a spočíáš "c"
Offline
#13 20. 12. 2009 23:34 — Editoval Doxxik (20. 12. 2009 23:35)
Re: help pls
mno co takhle vlastní návrh?
Offline
#21 21. 12. 2009 00:59
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: help pls
Nechtěla jsem narušovat průběh řešení - není to dobré, když se přeskakuje z jednoho postupu na jiný (zejména, když není jasné, jakou teoretickou základnu má autor dotazu) - tak jen odkaz na řešení přes směrnicový tvar přímek.
Pozdrav :-)
Offline
#22 21. 12. 2009 08:19
Re: help pls
↑ Doxxik:
Krásně jsi mu to vysvětlil. Jen bych tě chtěl upozornit, že když jsem vypočítal  , tak stačí dosadit do mé první rovnice
, tak stačí dosadit do mé první rovnice 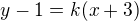 a upravit. Žádné
a upravit. Žádné  ani nic jiného už nemusím počítat. (A proto jsem taky použil tuto rovnici.)
ani nic jiného už nemusím počítat. (A proto jsem taky použil tuto rovnici.)
Pořádek je pro blbce, inteligent zvládá chaos!
Offline

![kopírovat do textarea $[-3;1]$](/mathtex/10/109c7bd4e72182a34b6e762ca6c202a3.gif) mají rovnici
mají rovnici 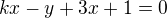 . Pro úhel, který svírá s přímkou
. Pro úhel, který svírá s přímkou 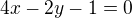 je
je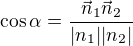 , tj
, tj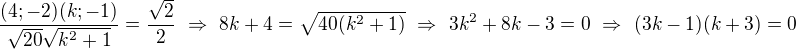
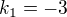 ,
,