Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 12. 2009 17:30
Řada (Děmidovič 2600)
Zdravím kolegy,
problém je s následující řadou: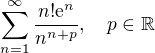
Limita z Raabeho kritéria dává 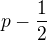 , takže pro
, takže pro  řada konverguje a pro
řada konverguje a pro  diverguje. Problém nastává pro
diverguje. Problém nastává pro 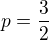 .
.
Srovnáním s divergentním  dostaneme limitu
dostaneme limitu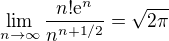
kde výsledek znám ovšem jen díky Stirlingově aproximaci.
Otázka zní: dá se divergence této řady ukázat i jinak, s elementárnějším aparátem?
Offline
#2 26. 02. 2010 14:33
Re: Řada (Děmidovič 2600)
↑ Olin:
Nebude tvůj problém řešit přístup, kde se pokusíme nějakým snadným způsobem dostat Stirlingův vzorec? Obecný tvar sčítance této řady předurčuje tuto formuli k použití při řešení otázek o konvergenci nebo divergenci řady.
Offline
#3 26. 02. 2010 15:30 — Editoval Rumburak (26. 02. 2010 16:34)
Re: Řada (Děmidovič 2600)
↑ Olin:
Mně to nevychází zase až tak složitě (tedy pokud tam nemám chybu):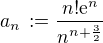 , takže
, takže 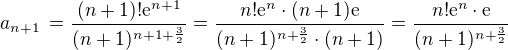 a
a 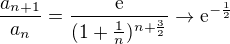 .
.
D´Alembert by potom dával konvergenci . (???)
EDIT. TENTO VÝPOČET JE ŠPATNĚ. Viz ↑ BrozekP:, ↑ Rumburak:
Jako odstrašující příklad to tu nechám.
Offline
#4 26. 02. 2010 15:36
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Řada (Děmidovič 2600)
Máš :-)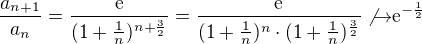
Offline
#5 26. 02. 2010 15:46 — Editoval Rumburak (26. 02. 2010 16:35)
Re: Řada (Děmidovič 2600)
↑ BrozekP:, ↑ Olin:
Díky, v roztržitosti jsem použil "vzorec" 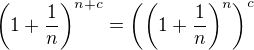 , který NEPLATÍ.
, který NEPLATÍ.
Offline