Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Důkaz B-C podmínky (TOTO TÉMA JE VYŘEŠENÉ)
#1 29. 12. 2009 11:26
Důkaz B-C podmínky
Zdravím kolegy,
důkaz B-C podmínky, který mám v sešitě zapsaný z přednášky, mi přišel příliš zdlouhavý a nenázorný - oproti tomu, který mě samotného napadl. Místo důkazu B-C podmínka splněna => a_n konverguje provádím důkaz a_n diverguje => B-C podmínka porušena. Připomínám, že B-C podmínka vypadá následovně:
Negace je
Prosím o kontrolu:
Je-li a_n neomezená, pak je podmínka zřejmě porušena - zvolíme si epsilon jakékoliv, n třeba n_0 a díky neomezenosti určitě můžeme najít takové m, že 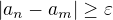 .
.
Pokud je a_n omezená, ale není konvergentní, pak má alespoň dva hromadné body, označím je X, Y, přičemž  . Zvolím
. Zvolím 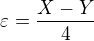 . Nechť
. Nechť 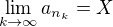 ,
, 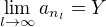 . Pro každé n_0 zvolím m, n tak, že
. Pro každé n_0 zvolím m, n tak, že  (můžu díky konvergenci) a analogicky
(můžu díky konvergenci) a analogicky  . Potom je
. Potom je  a
a  a podle volby epsilonu tedy dokonce
a podle volby epsilonu tedy dokonce  . Hotovo.
. Hotovo.
Offline
#2 29. 12. 2009 12:08
Re: Důkaz B-C podmínky
↑ Olin:
Keď sme mali dôkaz tejto vety, tak ma tiež napádali podobné riešenia. Dôkaz je skutočne zdĺhavý a spomínam si naň, že som ho nepochopil. V podstate vo svojom dôkaze rozoberáš vzdialenosti hromadných bodov cez podpostupnosti. Možno by si to vyžadovalo názor odborníka.
OT:
Tiež by som vrátil do pozornosti Řada (Děmidovič 2600). Riešenie je pekné, ale jednoduchšie som však nenašiel. Dokonca by ma nenapadlo ani uvažovať Stirlingov odhad.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#3 29. 12. 2009 12:33 — Editoval RobbieMan (29. 12. 2009 13:15)
Re: Důkaz B-C podmínky
na mff v matanalyze jsme si uvadeli obe implikace, pricemz ta prvni, tedy ta kterou si vymyslel je opravdu jednodussi a lepsi, ale trochu jsem se bal aby se me na to nezeptali na zkousce, tak jsem se naucil obe, v jarníkovi je ta tezsi implikace dobre vysvetlena, opravdu se to tam nejak resi pres lim inf a lim sup,
btw: jak jste se vyporadali s dukazem o n-té odmocnine?? pokud jste ji teda nekdo mel
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Důkaz B-C podmínky (TOTO TÉMA JE VYŘEŠENÉ)
