Matematické Fórum

spiderx · 31. 12. 2009 18:13

Můžete mi prosím pomoct s následující limitou?
lim┬(x→0+)⁡(1-e^(7x^2 ) )cotg^2 x
dostanu se do fáze, že ve jmenovateli je tg x * 1/cos^2x a dál nevím... měl bych z toho dostat sin x, ale nemůžu přijít na to, jak... díky za rady.

Stýv · 31. 12. 2009 20:35

z cotg(x) potřebuješ dostat sin(x)? co třeba cotg(x)=cos(x)/sin(x)?

spiderx

↑ Stýv:↑ Stýv:

ne z cotg. Ale z výrazu tg x * 1/cos^2x

Tento výraz potřebuji nějak upravit na sin x. A nevím jak.

Stýv · 31. 12. 2009 20:56

to asi nepůjde: $\frac{\tan x}{\cos^2x}\equiv\frac{\sin x}{\cos^3x}\not\equiv\sin x$

spiderx · 31. 12. 2009 22:36

↑ Stýv:

tak to je asi špatně spočítáno... dostal jsem výpočet pro nastudování, ale nemohl jsem přijít na to, jak se k tomu dobral...

Stýv · 31. 12. 2009 23:31

tam do toho kosinu patrně dosadil tu nulu

spiderx · 31. 12. 2009 23:38

↑ Stýv:

já vím, že je už pozdě... ale kam dosadil? To je přece jen nějak upravený tvar, konstanty vyhodil před limitu a jak došel k tomu sin x, to furt nechápu...

Stýv · 01. 01. 2010 01:19

do kosinu, jelikož cos(0)=1, tak prostě zmizí

spiderx

↑ Stýv:

asi si pořád nerozumíme... zvýraznil jsem červeně to, co nechápu, jak bylo provedeno.

je ta limita správně, nebo ne?

jelena · 02. 01. 2010 00:27

↑ spiderx:

Zdravím,

jak se používal v jednotlivých krocích l´Hospital - je to jasné? Po kroku, co máš vyznačeno červeně, za x dosazuji 0, čímž dostaváji cos(0)=1 na všech pozicích, kde je cosx (tedy i v tg(x)=sin(x)/cos(x)), pak už cos(x) úplně vynechali.

Osobně bych výraz vyznačený červeně bych přepsala jako 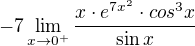$-7\lim_{x\rightarrow 0^{+}}\frac{x \cdot e^{7x^2}\cdot cos^3 x}{\sin x}$ , čímž dostanu 1 jako "převracenou" limitu ze sin (x)/x - viz pozoruhodné limity a jedničky na všech ostatních pozicích (po dosazení 0) - nechce se mi vypisovat. Může být?

spiderx · 02. 01. 2010 17:06

↑ jelena:

Ahoj, no tak tohle už je jasné, takhle přepsanému už rozumím, děkuju za pomoc.
Akorát tenhle výraz je zase [0/0], takže opět l'Hospital a já bych asi nechal to cos^3(x) ve jmenovateli, to se bude líp derivovat, než součin tří funkcí v čitateli, ne?
Jen pořád nemůžu pobrat, jak je možné, že to cos^3(x) se vynechá v tom skenovaném výpočtu a už se s ním nepočítá....

jelena · 02. 01. 2010 19:55

↑ spiderx:

no pravě proto se mi to příliš nelibí, že cos(x) je vynechan ve scanu a navrhuji tuto úpravu: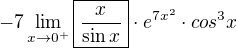

$-7\lim_{x\rightarrow 0^{+}}\boxed{\frac{x}{\sin x}}\cdot e^{7x^2}\cdot cos^3 x$ orámovanou část jsem označila za "převrácenou" "pozoruhodnou limitu" a je to poslední krok (žádný další l'Hospital není) - stačí tak?

spiderx

↑ jelena:

aha, takže platí lim x>0 sinx/x=1 <=> lim x>0 x/sinx=1 ???

pak by tedy byl výsledek -7*1=-7 správný?

jelena · 03. 01. 2010 00:21

↑ spiderx: přepiš si to takto:

$-7\lim_{x\rightarrow 0^{+}}\frac{e^{7x^2}\cdot cos^3 x}{\boxed{\frac{\sin x}{x}}}=-7$ uz v poradku?

halogan · 03. 01. 2010 00:27

Nebo využij aritmetiky:

Nechť existuje $A = \lim_{x \to c} f(x),\quad A \in R^*$ a $B = \lim_{x \to c} g(x),\quad B \in R^*$ , pak platí
$\lim_{x \to c} \frac{f(x)}{g(x)} = \frac{A}{B}$ ,
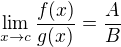pokud je výraz vpravo definován.

Přepíšeš si pak limitu:

$\lim_{x \to 0} \frac{x}{\sin x} = \lim_{x \to 0} \frac{1}{\frac{\sin x}{x}} = \frac{\lim_{x \to 0} 1}{\lim_{x \to 0} \frac{\sin x}{x}}$ ,

což je to stejné, jak navrhuje kolegyně, jen obecně. Stejně si pak můžeš převracet limitu typu (tan x)/x, x -> 0; (arcsin x)/x, x -> 0, ...

jelena · 03. 01. 2010 00:37

↑ halogan:

děkuji za doplnění - měla jsem za to, že převrácení u těchto limit je samozřejmost pravě v důsledku toho, že jsou to podíly.

Ale co je podstatné, v seznamu pozoruhodných některé pozoruhodné chybí, ovšem do vzorových se nedá nic přidávát, jen editovat - budu muset přiležitostně oslovit kolegu Lukáše.

spiderx · 03. 01. 2010 20:52

↑ jelena: ↑ halogan:

moc díky, už je to jasné.

jelena · 03. 01. 2010 21:06

↑ spiderx: děkuji za zprávu, kolega halogan bude jistě potěšen, když téma odfajfkneš jako vyřešené, děkuji.

halogan · 03. 01. 2010 21:10

Já si to fajfknu rád sám, i když jsem tu odvedl minimum práce :-)

Matematické Fórum

#1 31. 12. 2009 18:13

Limita nula x nekonečno

#2 31. 12. 2009 20:35

Re: Limita nula x nekonečno

#3 31. 12. 2009 20:44 — Editoval spiderx (31. 12. 2009 20:48)

Re: Limita nula x nekonečno

#4 31. 12. 2009 20:56

Re: Limita nula x nekonečno

#5 31. 12. 2009 22:36

Re: Limita nula x nekonečno

#6 31. 12. 2009 23:31

Re: Limita nula x nekonečno

#7 31. 12. 2009 23:38

Re: Limita nula x nekonečno

#8 01. 01. 2010 01:19

Re: Limita nula x nekonečno

#9 01. 01. 2010 23:03 — Editoval spiderx (01. 01. 2010 23:05)

Re: Limita nula x nekonečno

#10 02. 01. 2010 00:27

Re: Limita nula x nekonečno

#11 02. 01. 2010 17:06

Re: Limita nula x nekonečno

#12 02. 01. 2010 19:55

Re: Limita nula x nekonečno

#13 02. 01. 2010 20:48 — Editoval spiderx (02. 01. 2010 20:51)

Re: Limita nula x nekonečno

#14 03. 01. 2010 00:21

Re: Limita nula x nekonečno

#15 03. 01. 2010 00:27

Re: Limita nula x nekonečno

#16 03. 01. 2010 00:37

Re: Limita nula x nekonečno

#17 03. 01. 2010 20:52

Re: Limita nula x nekonečno

#18 03. 01. 2010 21:06

Re: Limita nula x nekonečno

#19 03. 01. 2010 21:10

Re: Limita nula x nekonečno

Zápatí