Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#76 27. 10. 2008 14:59
#78 12. 01. 2009 17:38
Offline
#80 02. 02. 2009 16:17
Re: slovní úlohy o pohybu
Čaute.
Prosím poradte nevím jak na to:
V řadě je vysázeno 17mladých stromků ve vzdálenosti 5m od sebe.U prvního se nachází studna.Jakou cestu vykonájestliže chodí se dvěma konvemi a coda z jedné konve stačí na zalití 2stromků?Práci ukončí opět u studny.
Offline
#81 02. 02. 2009 21:08
Re: slovní úlohy o pohybu
↑ majsner:
16 stromků má celkem na čtyři cesty (2 konve 4 stromky) mezi stromky je 5m ; 17tý stromek je zárověň se studnou , nemusí k němu chodit .
1. cesta ..(5*4 )m jde tam a zpět... 5*4*2=40m
2. cesta .. 5* 8*2 =80m ... tou dvojkou násobíme protože jde cestu dvakrát
3. cesta .. 5*12*2 =120m
4. cesta .. 5*16*2 = 160m
čísla 4,8,12,16 .. je počet stromků které míjí s konvemi na dvě konve čtyři stromky, přičemž v opakovaných cestách vždy čtyři potom osm a nakonec 12 míjí protože už jsou zalité.
Celkem tedy ujde 40+80+120+160=400m.
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#82 03. 02. 2009 06:58
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: slovní úlohy o pohybu
↑ Ivana:
Tady by se dala pěkně využít aritmetická posloupnost:
Cesty jsou celkem čtyři.
První cesta = 40 m = 2*4*5
Poslední cesta =160 m = 2*16*5
potom:
Obávám se, ale, že na základce se aritmetickou řadu neučí.
Nikdo není dokonalý
Offline
#83 15. 02. 2009 20:04
Re: slovní úlohy o pohybu
prosím, chtěla bych vás poprosit jestli byste mi nepomohli vyřešit tyto slovní úlohy
1.nákladní auto jelo prům. rychlostí 20km/h a vyjelo z Prahy směrem k Liberci, současně s ním vyjel autobus, který jel prům.rychlostí 30km/h a který přijel do Liberce o 2 hodiny dříve než nákladní auto, jaká je vzdálenost mezi Prahou a Libercem?
2.pumpou A se naplní nádrž za 12 minut, pumpou B za 24 minut, za jakou dobu se naplní nádrž, pracuje-li 3 minuty jen pumpa A a potom obě pumpy současně?
3.v 6 hodin 15 minut vyjela z kasáren kolona aut jedoucí prům. rychlostí 32 km/h, v 7 hodin 18 minut vyjelo za kolonou vojenské terénní vozidlo UAZ, vypočtěte, jakou prům. rychlostí musí terénní vozidlo jet, má-li do vojenského výcvikového prostoru, vzdáleného od kasáren 72 km, dorazit současně z kolonou
4.Z místa A do místa B je 25 a jedna třetina km. V 6 hodin ráno vyšel chodec S z místa A směrem do místa B. V 7 hodin 10 minut vyšel chodec Z z místa B směrem do místa A. Setkali se v 9 hodin. Kolik ušel průměrně za hodinu každý z obou chodců, jestliže chodec Z ušel za hodinu o 2 km méně než chodec S?
5.Auto ujelo vzdálenost mezi městy A a B za 4 hodiny. Kdyby se průměrná rychlost auta zvýšila o 17 km/h, ujelo by auto tuto vzdálenost o hodinu dříve. určete rychlost auta a vzdálenost mezi městy A a B.
6.Žáci 8. třídy ZŠ z města M uskutečnili výlet do místa N vzdáleného 74 km.Část cesty z M do N jeli vlakem prům. rychlostí 44 km/h a část cesty šli pěšky průměrnou rychlostí 4 km/h Cesta vlakem byla o 30 minut kratší než pěší túra. Za jakou dobu se žáci dostali z města M do města N?
Offline
#84 15. 02. 2009 22:18
Re: slovní úlohy o pohybu
↑ kaculicka:
Př. 1)
s - vzdálenost Praha Liberec
t - čas po, který pojede autobus
t + 2 čas, po který pojede nákladní auto (nákladní auto přijelo do Liberce o 2 hodiny později než autobus tj. bylo na trase o 2 hodiny déle)
Vzdálrnost ujela obě vozidla stejnou.
Platí: ze vztahu: 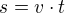
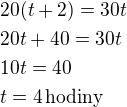
Autobus tedy jel z Prahy do Liberce 4 hodiny a za tuto dobu ujel:vzdálenost 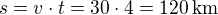
Vzdálenost Praha Liberec je 120 km.
Offline
#85 15. 02. 2009 22:27 — Editoval Chrpa (15. 02. 2009 22:27)
Re: slovní úlohy o pohybu
↑ kaculicka:
Př. 2)
Pumpou A se naplní nádrž za 12 minut. Znamená to, že za 3 minuty, po které pracuje pumpa samostatně se naplní 3/12 = 1/4 nádrže.
Pak pracují obě pumpy současně po dobu x minut. a musí naplnit 3/4 nádrže.
Sestavíme rovnici: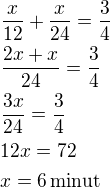
Společně tedy oběpumpy pracují 6 minut a dohromady se třemi minutami, kdy pracovala pumpa A sama je celkový čas plnění nádrže: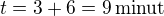
Nádrž se naplní za 9 minut.
Offline
#86 15. 02. 2009 22:39
Re: slovní úlohy o pohybu
↑ kaculicka:
Př. 3)
Označme
v - průměrnou rychlost UAZ (máme určit)
t - čas, po který pojede kolona a ujede 72 km.
Pak platí: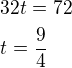
Protože UAZ vyjel o 1 hodinu a 3 minuty déle než kolona (7:18 - 6:15 = 1 hodina 3 minuty = 21/20 hodiny)
je jeho celkový čas dán vztahem: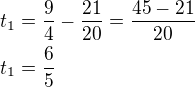
Za uvedený čas musí UAZ ujet rychlostí v vzdálenost 72 km tj: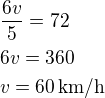
UAZ musí jet průměrnou rychlostí 60 km/h.
Offline
#87 15. 02. 2009 22:55
Re: slovní úlohy o pohybu
↑ Cheop:
Př.4)
Chodec S jde rychlostí v do doby setkání 3 hodiny (9 - 6 = 3)
Chodec Z jde rychlostí v - 2 do doby setkání 9 - 7:10 = 11/6 hodiny)
Oba dohromady musí ujít vzdálenost míst tj. 25a 1/3 km = 76/3 km.
Sestavíme rovnici:
Rychlost chodce S je 6 km/h.
Rychlost chodce Z je 6 - 2 = 4 km/h
Offline
#88 15. 02. 2009 23:00
Re: slovní úlohy o pohybu
↑ kaculicka:
Př 5)
Označme:
s - vzdálenost měst AB
v rychlost auta v prvním případě.
Ze zadání lze sestavit rovnice: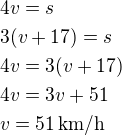
Průměrná rychlost auta je 51 km/h.
Dopočteme vzdálenost měst AB
Vzdálenost měst je 204 km.
Offline
#89 15. 02. 2009 23:14 — Editoval Chrpa (15. 02. 2009 23:15)
Re: slovní úlohy o pohybu
↑ kaculicka:
Př. 6)
Označme:
t - čas ve vlaku
t + 1/2 - čas pěší túry.
Celkový čas výletu tedy bude t + t +1/2 = 2t + 1/2 hodiny.
Musí platit:
Cesta vlakem tedy trvala 1,5 hodiny . Pěší túra byla o 30 minut delší tj. Pěší túra trvala 1,5 + 0,5 = 2 hodiny.
Celý výlet tedy trval:
1,5 + 2 = 3,5 hodiny.
Žáci se z města M do města N dostali za 3 hodiny 30 minut.
Offline
#91 16. 02. 2009 11:50 — Editoval Cheop (16. 02. 2009 11:51)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: slovní úlohy o pohybu
↑ kaculicka:
Př. 2) by lépe šel počítat takto:
Označme x - doba, po kterou je pumpa A v chodu (minut)
pak x - 3 - doba , po kterou je v chodu pumpa B (pumpu B jsme pustili o 3 minuty později než pumpu A)
Sestavíme rovnici
Nádrž se naplní za 9 minut.
Nikdo není dokonalý
Offline
#93 25. 03. 2009 16:59
- tajemnaholka
- Příspěvky: 39
- Reputace: 0
Re: slovní úlohy o pohybu
halo potřebuji pomoc s tou to úlohou mám jí mít zítra do školy. Tady je : V 6 hodin 40 minut vyplul z přístavu parník plující průměrnou rychlostí 12 km/h. Přesně v 10 hodin za ním vyplul motorový člun km průměrnou rychlostí 42 km/h. V kolik hodin av jaké vzdálenosti dohoní člun parník?Potřebovala bych i náčrtek a postup a tak. Děkuji předem a napište
Offline
#94 25. 03. 2009 17:39
- tajemnaholka
- Příspěvky: 39
- Reputace: 0
Re: slovní úlohy o pohybu
potřebovala bych vypočítat tu to slovní úlohu:V 6 hodin 40 minut vyplul z přístavu parník plující průměrnou rychlostí 12 km/h. Přesně v 10 hodin za ním vyplul motorový člun km průměrnou rychlostí 42 km/h. V kolik hodin a v jaké vzdálenosti dohoní člun parník? Potřebovala bych náčrtek a postup. Papapa
Offline
#95 25. 03. 2009 17:47 — Editoval Chrpa (25. 03. 2009 22:10)
Re: slovní úlohy o pohybu
↑ tajemnaholka:
Máš to vypočítáno od ttopi jiném vlákně.
Sem přidám obrázek
Rozdíl ve vyplutí parníku a člunu je 10:00 - 6:40 =3 hodiny 20 minut = 10/3 hodiny
Za 10/3 hodiny ujede parník při rychlosti 12 km/h vzdálenost 12*10/3 = 40 km.
V tomto momentě vyjede člun rychlostí 42 km/h. a pojede čas t než dojede parník.
Za čas t ujede parník rychlostí 12 km/h vzdálenost 12t
Za čas t ujede člun rychlostí 42 km/h vzdálenost 42t
Rozdíl ve vzdálenosti je 40 km
Platí tedy:
42t = 12t+40
42t - 12t = 40
30t=40
t = 4/3 hodiny.
Člun byl tedy na cestě, než dojel parník, 4/3 hodiny tj. 1 hodina 20 minut
Vyjel v 10:00 a parník dojel v 11:20 (10 + 1:20 = 11:20)
Při rychlosti 42 km/h ujel za uvedený čas vzdálenost: s = 42*4/3 = 56 km.
Odpověď zní:
Člun dohonil parník v 11:20 ve vzdálenosti 56 km od místa vyplutí.
Offline
#96 03. 10. 2009 16:01
Re: slovní úlohy o pohybu
Ahoj, já bych potřebovala poradit s touto úlohou: Z Berouna vyjelo v 7h. směrem na Prahu po dálnici v mlze nákladní auto. Za 20min. po něm, ze stejného místa a po stejné trase, vyjelo osobní auto rychlostí o 27km/h větší. Osobní auto přednjelo nákladní auto po dalších 20min. Jaké byli rychlosti obou aut? pořád mi to nějak nevychází... prosím jestli někdo víte tak napište
Offline
#97 03. 10. 2009 16:43 — Editoval Chrpa (03. 10. 2009 18:04)
Re: slovní úlohy o pohybu
↑ Len!nka:
Označme:
v - rychlost nákladního auta
v + 27 - rychlost osobního auta (osobní auto jelo o 27 km/h rychleji než nákladní auto)
Nákladní auto bylo na cestě 20 + 20 = 40 minut = 2/3 hodiny (vyjelo před osobním autem o 20 minut dříve a to jej dohonilo za dalších 20 minut)
Osobní auto bylo na cestě 20 minut = 1/3 hodiny
Obě auta ujela stejnou vzdálenost
Můžeme sestavit rovnici: podle vzorce s = v.t, kde v je rychlost, t je čas a s je vzdálenost 
Rychlost nákladního auta byla 27 km/h
Rychlost osobního auta bude:
Rychlosti aut jsou: 27 km/h (nákladní) a 54 km/h(osobní)
Offline
#98 04. 01. 2010 17:58
Re: slovní úlohy o pohybu
Ahojte dnes se už hodinu trápím s tímto příkladem a pořád mi vycházejí výsledky prosím rychlou pomoc zítra to potřebuji do školy :-( takže
Cyklista vyjel z města rychlostí 18km/h za 1,5 vyjel za ním automobil týmž směrem a dohonil cyklistu za 50 min . Jakou rychlostí jel automobil ?
Prosím poradte
Offline
#99 04. 01. 2010 18:29 — Editoval Chrpa (04. 01. 2010 18:40)
Re: slovní úlohy o pohybu
↑ Honzas:
Celková doba jízdy cyklisty je 1,5 + 5/6 =7/3 hodiny
Za tu dobu ujel rychlostí 18 km/h vzdálenost 18*7/3 = 42 km.
Automobil musel ujet tu samou vzdálenost (nakonec ho dojel) tj. ujel taky 42 km. Potřeboval na to 50 minut = 5/6 hodiny
Jeho rychlost je: 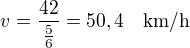
Rovnicí by to bylo: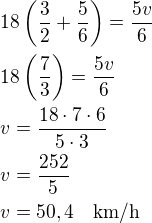
Offline
#100 04. 01. 2010 18:46
Re: slovní úlohy o pohybu
Děkuji za bleskovou odpověd a ještě promin že otravuji ale mám tu další se kterým si nevím rady a poslední :)
Obchodník objednal 200 broušených sklenic Výrobce potvrdil objednávku s tím žw sklenice pošle v krabicích jako soupravy obsahující bud po čtiři nebo šest sklenic celkem pošle 41 krabic
A)Kolik krabic bude obsahovat pouze 4 sklenice
?B) kolik krabic bude obsahovat 6 sklenic .?
Offline



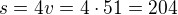 a ne
a ne 