Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 01. 2010 14:07
grupa afinit
prosim o pomoc
1, jak vypada nejmensi podgrupa grupy A2, která obsahuje afinitu danou maticí E = /1, 1, 0, 1/
2, najdete nutou a postacujici podminku pro to, aby afinita f z A2 dana matici X = /a, b, c, d/
dekuji
Offline
- (téma jako vyřešené označil(a) Kondr)
#2 05. 01. 2010 16:31
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: grupa afinit
↑ Matik: Afinita je daná maticí M a vekorem v -- vektoru u pak přiřazuje vektor Au+v. Máme to brát tak, že vektor v je v obou otázkách nulový?
Druhá otázka nedává smysl (chybí přísudek).
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#4 05. 01. 2010 19:29
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: grupa afinit
V tom případě to budeme brát tak, jak jsem naznačil: že vektor v budeme považovat za nulový.
1) Skládání afinit odpovídá násobení matic. Protože má být grupa uzavřená na skládání, v řeči matic to znamená uzavřenost na násobení. Grupa musí obsahovat afinity dané maticemi 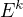 , kde
, kde  je celé číslo (
je celé číslo (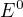 je jednotková matice). Tyto matice se dají explicitně popsat -- stačí spočítat
je jednotková matice). Tyto matice se dají explicitně popsat -- stačí spočítat 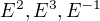 a mělo by to být jasné.
a mělo by to být jasné.
2) Pro danou matici má platit  a přitom X není jednotková. Když to rozepíšeme, máme 4 rovnice pro 4 neznámé, neměl by být problém je vyřešit a vyloučit jednotkové řešení.
a přitom X není jednotková. Když to rozepíšeme, máme 4 rovnice pro 4 neznámé, neměl by být problém je vyřešit a vyloučit jednotkové řešení.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#6 05. 01. 2010 21:19
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: grupa afinit
↑ Matik: Násobit matice umíš? Jestli jo, tak zkus spočítat E^2=E*E a E^3=E*(E*E), to by tě mělo nakopnout k té jedničce. Kdyžtak sem napiš, jak vyšla E^3, ať se máme od čeho odrazit.
U dvojky -- X*X vyjde  . Protože se to má rovnat jednotkové matici, máme rovnosti
. Protože se to má rovnat jednotkové matici, máme rovnosti
Jsou dvě možnosti
1)  . Pak b zvolíme libovolné nenulové a z první rovnice
. Pak b zvolíme libovolné nenulové a z první rovnice 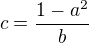 , a zvolíme téý libovolně, d=-a. Nulové
, a zvolíme téý libovolně, d=-a. Nulové  lze volit jen pro
lze volit jen pro 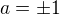 , v takových případech může být c libovolné.
, v takových případech může být c libovolné.
2) 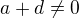 . Pak ze druhé a třetí rovnice b=c=0, z první a druhé
. Pak ze druhé a třetí rovnice b=c=0, z první a druhé 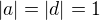 . Protože jednotková matice nás nezajímá, je řešením v tomto případě pouze
. Protože jednotková matice nás nezajímá, je řešením v tomto případě pouze 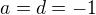 .
.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#8 05. 01. 2010 21:38
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: grupa afinit
↑ Matik: Výborně :) Takže hypotéza je E^n=<1,n,0,1>. Bázový krok (pro n=0) máme. Předpokládejme, že platí pro n=k, pro n=k+1 dokážeme snadno:
E*E^k=<1,1,0,1>*<1,k,0,1>=<1,k+1,0,1>. Tím bychom ji měli dokázanou pro nezáporná čísla. Pro záporná to už je snadné E^(-k)=(E^k)^(-1)=<1,-k,0,1> (rychloinvertování matic 2*2: na hlavní diagonále prohodíme prvky, na vedlejší změníme znaménka a výsledek dělíme determinantem).
V dané grupě musí být afinity dané maticemi <1,n,0,1>. Na druhou složením dvou takovýchto afinit dostaneme také takovouto afinitu, inverzí opět nedostaneme nic jiného. Nejmenší grupa je tedy {afinita daná maticí <1,n,0,1>| n je celé}.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#10 05. 01. 2010 22:42
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: grupa afinit
Každou elaci lze vzhledem k vhodně zvoleným souřadnicím zadat maticí  . Je proto složením afinit daných maticemi
. Je proto složením afinit daných maticemi  a
a  , které jsou involucemi (viz přechozí příspěvek nebo umocněním matice na druhou) a afinitami.
, které jsou involucemi (viz přechozí příspěvek nebo umocněním matice na druhou) a afinitami.
BRKOS - matematický korespondenční seminář pro střední školy
Offline