Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Důkazy z diskrétní matematiky (TOTO TÉMA JE VYŘEŠENÉ)
#1 02. 01. 2010 16:48 — Editoval Olin (02. 01. 2010 16:50)
Důkazy z diskrétní matematiky
Zdravím kolegy,
jako přípravu na blížící se zkoušku si cvičně dokazuji tvrzení, která jsou v mém sešitě nebo v Kapitolách z diskrétní matematiky. Prosím o kontrolu:
1. Každá konečná částečně uspořádaná množina má minimální prvek.
Důkaz zcela vymyšlený mnou, dost krkolomný. Nevím, jestli v něm není nějaký kruh.
Sporem: nechť 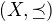 je konečná částečně uspořádaná množina, která nemá žádný minimální prvek, tj.
je konečná částečně uspořádaná množina, která nemá žádný minimální prvek, tj. 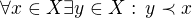 , kde
, kde  je ostrá verze
je ostrá verze  . Nechť tedy
. Nechť tedy  je zobrazení v
je zobrazení v  takové, že
takové, že 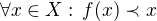 . Označme
. Označme 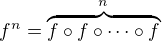 . Zřejmě je
. Zřejmě je 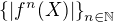 nerostoucí posloupnost přirozených čísel, existuje tedy taková
nerostoucí posloupnost přirozených čísel, existuje tedy taková 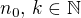 , že
, že 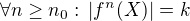 . Protože k-prvkových podmnožin
. Protože k-prvkových podmnožin  je jen konečně mnoho, existují taková
je jen konečně mnoho, existují taková  , že
, že  . Z toho plyne, že
. Z toho plyne, že  je bijekce (permutace) na množině
je bijekce (permutace) na množině  . Existuje tedy takové
. Existuje tedy takové 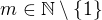 a
a  , že
, že  , jelikož permutace vždy obsahuje cyklus (na požádání dokážu :-) ). Protože ale
, jelikož permutace vždy obsahuje cyklus (na požádání dokážu :-) ). Protože ale  zobrazí každý prvek na nějaký ostře "menší", platí
zobrazí každý prvek na nějaký ostře "menší", platí 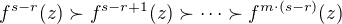 , což je spor s tím, že
, což je spor s tím, že 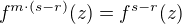 .
.
2. Pro každé částečné uspořádání na konečné množině 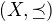 existuje lineární uspořádání
existuje lineární uspořádání 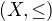 takové, že
takové, že 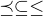 , tj. každé částečné uspořádání lze na konečné množině zúplnit na lineární.
, tj. každé částečné uspořádání lze na konečné množině zúplnit na lineární.
V mém sešitě je důkaz proveden indukcí podle velikosti  , a tak jsem ji zvolil také.
, a tak jsem ji zvolil také.
1. Pro 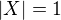 zřejmé (každé uspořádání na 1 prvku je lineární).
zřejmé (každé uspořádání na 1 prvku je lineární).
2. Víme pro 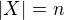 , chceme pro
, chceme pro  . Nechť
. Nechť  je nějaký minimální prvek v uspořádání
je nějaký minimální prvek v uspořádání  . Označme
. Označme 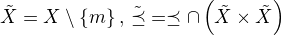 Jelikož
Jelikož 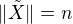 , existuje podle indukčního předpokladu lineární uspořádání
, existuje podle indukčního předpokladu lineární uspořádání 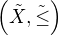 tak, že
tak, že 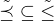 . Uspořádání
. Uspořádání 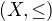 definujeme jako
definujeme jako 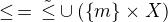 . Jde zřejmě o lineární uspořádání s nejmenším prvkem
. Jde zřejmě o lineární uspořádání s nejmenším prvkem  . Zbývá ověřit
. Zbývá ověřit 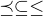 . Nechť
. Nechť 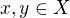 ,
, 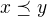 . Pokud
. Pokud 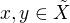 , pak
, pak 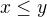 , protože
, protože  . Pokud
. Pokud  a
a  , je
, je 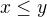 podle definice
podle definice 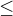 . Alternativa
. Alternativa 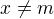 ,
,  nemůže nastat, protože
nemůže nastat, protože  je minimální prvek. Konečně pokud
je minimální prvek. Konečně pokud  , je platnost zřejmá.
, je platnost zřejmá.
Dost pravděpodobně přidám brzy ještě další důkazy.
Offline
- (téma jako vyřešené označil(a) Olin)
#2 02. 01. 2010 17:08
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Důkazy z diskrétní matematiky
↑ Olin: Oba důkazy vypadají OK. Nebylo by i to první rychlejší indukcí?
Pro |X|=1 platí.
Pro |X|=k+1 vybereme prevek a, uspořádání redukované na 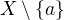 má dle IP minimální prvek b. Pokud je a<b, je a minimální prvek na X, pokud je b<a nebo jsou a,b neporovnatelné, je b minimální prvek na X.
má dle IP minimální prvek b. Pokud je a<b, je a minimální prvek na X, pokud je b<a nebo jsou a,b neporovnatelné, je b minimální prvek na X.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#3 02. 01. 2010 17:43
Re: Důkazy z diskrétní matematiky
↑ Kondr:
No jo, samozřejmě že je to tak jednodušší. Úvaha byla: "Je přece blbost, aby nějaká ČUMa neměla minimální prvek. Blbosti vedou ke sporu."
Teď jdu na důkaz věty "o dlouhém a širokém".
Offline
#4 03. 01. 2010 12:42 — Editoval Olin (03. 01. 2010 12:44)
Re: Důkazy z diskrétní matematiky
Tak posílám ten "slibovaný" důkaz.
3. Nechť 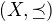 je částečné uspořádání,
je částečné uspořádání,  značí délku maximálního antiřetěžce (nezávislosti, velikost max. nezávislé množiny) a
značí délku maximálního antiřetěžce (nezávislosti, velikost max. nezávislé množiny) a 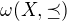 délku maximálního řetězce v tomto uspořádání. Pak platí
délku maximálního řetězce v tomto uspořádání. Pak platí  .
.
Indukcí podle 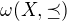 :
:
1.  .
.
2. 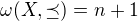 . Nechť
. Nechť  je množina všech minimálních prvků z
je množina všech minimálních prvků z 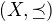 . Jde zřejmě o antiřetěz, protože z minimality všech prvků plyne pro
. Jde zřejmě o antiřetěz, protože z minimality všech prvků plyne pro 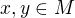 :
:  . Označme
. Označme  . Platí
. Platí 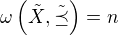 , protože odebráním všech minimálních prvků jsme všechny maximální řetězy v
, protože odebráním všech minimálních prvků jsme všechny maximální řetězy v  zkrátili o jeden prvek. Podle IP je
zkrátili o jeden prvek. Podle IP je  . Rozebereme dva případy:
. Rozebereme dva případy:
i) 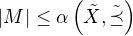 . Potom je
. Potom je 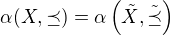 , takže
, takže  .
.
ii)  . Potom je
. Potom je  , takže
, takže 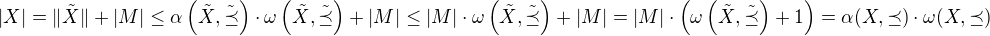 .
.
Offline
#6 07. 01. 2010 12:28
Re: Důkazy z diskrétní matematiky
↑ Kondr:
Díky, já taky ne, jen jsem to opět dělal možná zbytečně složitě - je zbytečné diskutovat velikost množiny  , protože vždycky musí platit
, protože vždycky musí platit 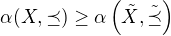 .
.
Každopádně teď jsem se vrátil ze zkoušky z diskrétky a snad by to měl být plný počet bodů, takže už asi další důkazy posílat nebudu. Na druhou stranu, kolega Halogan je průkopníkem nového žánru - skripta jako téma na fóru. Že bych se přidal? :-)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Důkazy z diskrétní matematiky (TOTO TÉMA JE VYŘEŠENÉ)