Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 12. 2009 13:04
Nekonečné řady
Ahoj,
kdo má nekonečné řady "v malíčku", mohl by se mrknout na můj pokus. Potřebuji to mít ke zkoušce dobře, ale nemá mi to kdo zkontrolovat. Díky moc (pozor, je to soubor pdf a celkové velikosti 1,5MB).
Díky moc
Marek
raduzak.kvalitne.cz/VPMA.pdf
Offline
#2 29. 12. 2009 14:42 — Editoval gladiator01 (29. 12. 2009 14:47)
- gladiator01


- Místo: Jindřichův Hradec
- Příspěvky: 1587
- Škola: ZČU FAV - SWI
- Pozice: absolvent
- Reputace: 53
- Web
Re: Nekonečné řady
Postup jsem nekontrolovala, ale výsledky by měli být dobře.
Můžeš si to zkontrolovat třeba zde: http://www.wolframalpha.com zadej např. sum(abs(n/(n^2+1)), n = 1 .. infinity)
Naděje jako svíce jas, potěší srdce štvané, čím temnější je noční čas, tím zářivěji plane.
VIVERE - MILITARE EST (Seneca)
Vím, že nic nevím. - Sokrates
Offline
#3 30. 12. 2009 07:11
Re: Nekonečné řady
↑ gladiator01: Díky, výsledek jsem si tam samozřejmě kontroloval, ale postup tam z 90% zkontrolovat nejde. Z matematiky už jsem celkem vypadl, tak nevím, jestli mám správně limity, integrály, apod. Ale díky.
Marek
Offline
#4 30. 12. 2009 13:53
Re: Nekonečné řady
Ahoj , potřebovala bych něco malinko vysvětlit, protože sama na to nějak nemůžu přijít :-(
suma {n = 0} {oo} (-8)^n / n!
Máme zjistit zda číselná řada konverguje nebo diverguje a také zda konverguje absolutně.
A ještě bych se chtěla zeptat na návod k této otázce.
Kolik sčítanců této řady bychom museli sečíst, abychom získali součet s přesností na tři desetinná místa?
Tady je můj výtvor:
lim {n -> oo} (-8)^n+1 / (n + 1)! * n! / (-8)^n = (-8)^n+1 * n! / (n + 1)! (-8)^n - odtud teď prostě nevím nějak jak dál
Moc díky za vaši pomoc..
Offline
#12 23. 01. 2010 20:50
Re: Nekonečné řady
↑ 99:
Je něco nejasného na nápisu
TOTO TÉMA JE VYŘEŠENÉ!
Pokud si nejste jisti, že Váš příspěvek navazuje na diskusi v tomto tématu, založte si prosím téma vlastní.
Offline


 znamená, že konverguje i
znamená, že konverguje i 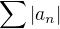
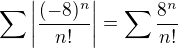 . ta limita vyjde 0, a jelikož 0<1, tak ta řada konverguje
. ta limita vyjde 0, a jelikož 0<1, tak ta řada konverguje