Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » eulerovo číslo, napierova konstanta (TOTO TÉMA JE VYŘEŠENÉ)
#1 18. 02. 2010 18:04 — Editoval [ReD]mikl (18. 02. 2010 18:17)
eulerovo číslo, napierova konstanta
ahoj, doufám, že naierova se opravdu píše takhle :D ale k mému dotazu:
jsem student gymnázia, jsem v sextě, jestli budu mít dotazy každý den dva, tak už to asi nebudu psát :D
derivace, logaritmy, integrály, faktoriály
po tom, co jsme skončili obecné záležitosti matematiky, jako rovnice (kvadratické...)..., myslím tím všechnu látku dosud, nyní bereme fce, lineární není problém, kvadratická také v pohodě, ale exponenciální to už je pro mě vyšší matematika, zajímám se o toto všechno, ale nemám nikoho s kým bych se mohl otevřeně bavit a kdo mi by odpověděl na všechny dotazy (učitel fyziky je sice nabušená hlava, ale pako a nikdo z učitelů nebude plýtvat časem když můžou být doma:D
1)přemýšlel jsem nad tímto: máme exp fci obecnou, bez eulera y = a na xtou (v texu neumím srry), Df = (1, oo), kladu si otázku: co když bude Df = R? Pokud bude a záporné, tak pro liché hodnoty x bude hodnota záporná a když x bude sudé, tak bude hodnota kladná, to znamená jediné, představme si graf fce y = - a na xtou: ( teď neřeším zda je a od nuly do jedné, nebo od jedné do oo) pokud budeme uvažovat a > 1 tak normální exp fce bude stoupající s bodem [0,1], a kdz6 bude -a, tak budou dvě "čáry" souměrné podle osy x ovšem to nebudou souvislé čáry, ale budou se skládat z nekonečně mnoha bodů, protože když vezmu interval třeba (1,2) tak lze do nejkonečna počítat desetinná čísla v tomto intervalu a když to bude třeba 1,1 tak to je liché, takže hodnota fce y = -1 na xtou bude pod osou x, když bude x 1,2 - sudé, tak hodnota bude nad osou x a takhle postupuju dál 1,11 1,12.... takže tato funkce existuje ne? je to čistě výtvor mé hlavy, učitelka říkala, že to nikdy neviděla a že se zamyslí nad tím, ale čas šel a nic :D tak se ptám tady, nevím zda to chápete, budou to body, jak nad osou tak souměrně pod osou x, nekonečně mnoho bodů nepropojených protože mezi jakýmykliv dvěma lichými číslicemi je jedna sudá (je jich tam nekonečně mnoho, ale když budu brát jendoduše 1,1 a 1,3 tak tak je 1,2, nebo když to bude 0,000001 a 0,000003 tak mezi nimi je sudá, a takhle zmenšuju do nekonečna, takže s těmi body mám pravdu ne? bude takhle vypadat ten graf ne? jeslti mám pravdu, byl ybch moc rád :D
další dotazy připojím potom
kdyby to nebylo jasné, tak udělám náčrt oskenuju ho a dám ho sem, tak díky
jo ještě upřesnění, nebudou souměrné podle osy x jelikož jedné hodnotě nad osou ( uděláme kolmici k ose x která prochází hodnoutou námi vybranou) tak pod osou ve stejné vzdálenosti nebude hodnota, budou dvě vedle a to záporné, neboli pro lichá x
a ještě omluva: nesouvisí to s eulerem
Offline
- (téma jako vyřešené označil(a) [ReD]mikl)
#2 18. 02. 2010 19:24
Re: eulerovo číslo, napierova konstanta
↑ [ReD]mikl:
Ahoj, tuto funkci jsem shodou okolností měl u maturity na gymplu. Ale to, co jsi definoval není exponenciální funkce. Ta je definována pouze pro a>0 a různé od 1. Nicméně funkce to je. Ale má komplexní a reálnou část. 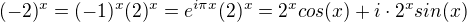 . Takže s Eulerem to souvisí-pokud tě to zajímá víc, pak si najdi něco o zlaté rovnici matematiky-to jsou ty čáry s tim e.
. Takže s Eulerem to souvisí-pokud tě to zajímá víc, pak si najdi něco o zlaté rovnici matematiky-to jsou ty čáry s tim e.
Do prázdného domu vešli 4 lidé, poté odešlo 6 lidí. Kolik lidí musí do domu vejít, aby byl dům prázdný?
Offline
#3 18. 02. 2010 19:38
Re: eulerovo číslo, napierova konstanta
Eště je dobré si uvědomit, že při zobrazení do reálné množiny čísel to není spojitá funkce, ale při zobrazení do komplexních ano.
Dotaz pro ostatní matematiky: ještě jsem neabsolvoval matematiku komplexních čísel a tedy nevím, zda pro komplexní funkci zavádíme pojem (tedy existuje) inverzní funkce?
Do prázdného domu vešli 4 lidé, poté odešlo 6 lidí. Kolik lidí musí do domu vejít, aby byl dům prázdný?
Offline
#4 18. 02. 2010 19:40
Re: eulerovo číslo, napierova konstanta
↑ [ReD]mikl:
A co třeba s čísly  a nebo
a nebo 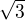 ? Ty nemají poslední cifru ani nelze určit jestli by byla lichá nebo sudá :)
? Ty nemají poslední cifru ani nelze určit jestli by byla lichá nebo sudá :)
Můžeš se podívat sem na graf funkce 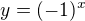 v komplexním oboru.
v komplexním oboru.
Offline
#5 18. 02. 2010 20:09 — Editoval [ReD]mikl (18. 02. 2010 20:10)
Re: eulerovo číslo, napierova konstanta
to je ten problém, že komplexní čísla jsme nebrali, a také je pravda, že jsem nepřemýšlel nad čísly iracionálními jako odmocniny, zlomky, takže děkuji za upozornění
jen mě zajímá jedno: vypadala by ta fce tak, jak jsem napsal?
děkuji všem za pomoc
ale na wolframu ty grafy vypadají jinak, je to tím, že je to v jiné množině čísel? té komplexní? jinak se to rozchází s mým předpokladem :D
Offline
#7 19. 02. 2010 19:54 — Editoval BrozekP (19. 02. 2010 19:55)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: eulerovo číslo, napierova konstanta
↑ [ReD]mikl:
Derivace je zjednodušeně směrnice tečny v daném bodě. Čím větší derivace, tím rychleji funkce v bodě rostě - je strmější.
(Je ta limita, ne ten limit :-) )
Offline
#8 19. 02. 2010 20:02
Re: eulerovo číslo, napierova konstanta
↑ Asinkan:
Inverzní funkce (zobrazení) vždy existuje pro nějakou prostou funkci. Třeba pro komplexní funkci  existuje inverzní, ale pro
existuje inverzní, ale pro  nikoliv, jelikož není prostá (na rozdíl od analogické funkce v reálných číslech).
nikoliv, jelikož není prostá (na rozdíl od analogické funkce v reálných číslech).
Offline
#9 19. 02. 2010 21:06
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: eulerovo číslo, napierova konstanta
[ReD]mikl napsal(a):
jsem nepřemýšlel nad čísly iracionálními jako odmocniny, zlomky
Iracionální zlomky z principu být nemohou, jen taková hnidopišská poznámka.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#11 20. 02. 2010 10:54
Re: eulerovo číslo, napierova konstanta
Derivace je jedním slovem ZMĚNA. Čím větší má funkce v daném místě derivaci-tím více se mění. Proto mají konstanty nulovou derivaci.
Do prázdného domu vešli 4 lidé, poté odešlo 6 lidí. Kolik lidí musí do domu vejít, aby byl dům prázdný?
Offline
#12 20. 02. 2010 15:47
Re: eulerovo číslo, napierova konstanta
↑ [ReD]mikl:
Jak jsi ve své úvaze přišel na to, že 1,1 je liché číslo a 1,2 sudé?
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » eulerovo číslo, napierova konstanta (TOTO TÉMA JE VYŘEŠENÉ)