Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » analýza - limity posloupností (TOTO TÉMA JE VYŘEŠENÉ)
#1 20. 11. 2010 19:07
analýza - limity posloupností
Ahoj, našel by se tu někdo, kdo by mi pomohl s přípravou na písemku z analýzy? Byl bych vám vděčný a určitě nejen já :)
http://www.karlin.mff.cuni.cz/~zajicek/UKAZKOVE2.pdf
Můj postup:
1) Použil jsem větu o vybraných posloupnostech a dokázal, že limita neexistuje.
2) Tady bych potřebval poradit, jak postupovat. Zaprvé nevím, co dělat s výrazem n*4^n a zadruhé potom nevím, co s tou odmocninou. + ještě bude potřeba použít větu o sevřených posloupnostech na tu doní část.
3) Tady jsem taky použil větu o sevřených posloupnostech na dolní část, potom jsem vytknul sqrt(n!) a vyšlo mi +nekonečno.
4) Limita toho zlomku za závorkou jde k nule zleva. Limita druhého zlomku v závorce jde ke dvojce a sinus je omezen (-1,1), takže bych řekl, že výsledek bude mínus nekonečno.
5) Devítky se zbavím tím, že to roztrhnu na dva zlomky. Ten zlomek s devítkou v čitateli jde k nule a na druhý zlomek nasadím rozšíření a dostanu 3/2.
6) Tady si nejsem úplně jistý, co mám dělat s tou n-tou odmocninou...
7) Ty odmocniny jsem rozšířil a vyšla mi nula. Stejně tak ten zlomek s faktoriálem jde k nule. Takže mi vyšla 0.
Předem díky za jakoukoliv pomoc a radu :)
Offline
- (téma jako vyřešené označil(a) FailED)
#6 21. 11. 2010 15:24
Re: analýza - limity posloupností
↑ llluk:
2) Něco jsi tam dokazoval pro 1/2, z toho ale neplyne že by to platilo pro každé epsilon, navíc nevím jak se ti tam dostala ta jednička k odmocnině napravo. V tom posledním kroku, proč by se měla změnit nerovnost když přidáš do té odmocniny napravo 1/2?
3) Je tam početní chyba,  , nemůžeš výraz jen tak nahradit nějakou jeho limitou! Jinak by to snad mohlo být ok.
, nemůžeš výraz jen tak nahradit nějakou jeho limitou! Jinak by to snad mohlo být ok.
6)  Jsi odhadnul shora, limita může být menší nebo rovna limitě toho odhadu!
Jsi odhadnul shora, limita může být menší nebo rovna limitě toho odhadu!
Když už, tak  .
.
Výsledek je dobře.
Bohužel vůbec nemám čas takže zbytek přenechávám kolegům.
Offline
#10 24. 11. 2010 21:57
Re: analýza - limity posloupností
↑ Mr.Pinker:
Myslíš tvrzení  ?
?
Platí
a tedy
navíc

 .
.
Nebo něco přehlížím?
Offline
#13 25. 11. 2010 17:53
Re: analýza - limity posloupností
prosimvas kde mam chybu: limity jsem si rozdelil na 9/jmenovatel coz jde k nule + ![kopírovat do textarea $\sqrt[3]{n^3+3n^2}-\sqrt{n^2-n}/jmenovatel$](/mathtex/22/22a7fa0eac3a4163698006bf7c5388ee.gif)
v citateli dostanu ![kopírovat do textarea $\sqrt[6]{(n^3+3n^2)^2}-\sqrt[6]{(n^2-n)^3}= \sqrt[6]{n^6+6n^5+9n^4}-\sqrt[6]{n^6-3n^5+3n^4-n^3}$](/mathtex/a6/a61b8df865b27fe001d1cce2c973c552.gif)
ted jsem to umocnil takze v citateli zbude 
ve jmenovateli mam ![kopírovat do textarea $((\sqrt[6]{n^6+6n^5+9n^4})^5+(\sqrt[6]{n^6+6n^5+9n^4})^4*\sqrt[6]{n^6-3n^5+3n^4-n^3}+...+(\sqrt[6]{n^6-3n^5+3n^4-n^3})^5) *(\sqrt{n}-\sqrt[3]{n})$](/mathtex/b8/b82b78e1270f8d39513fac5aa5464a48.gif)
nyni k celemu vyrazu opet rozdelim tentokrat na ![kopírovat do textarea $\frac{\sqrt{9n^5+6n^4+n^3}}{((\sqrt[6]{n^6+6n^5+9n^4})^5+(\sqrt[6]{n^6+6n^5+9n^4})^4*\sqrt[6]{n^6-3n^5+3n^4-n^3}+...+(\sqrt[6]{n^6-3n^5+3n^4-n^3})^5) } *\frac{\sqrt{9n^5+6n^4+n^3}}{(\sqrt{n}-\sqrt[3]{n})}$](/mathtex/38/384449cec346decd81e5ab770763c6c1.gif)
v obou citatelich vytknu  v prvnim jmenovateli vytknu n, ve druhem jmenovateli
v prvnim jmenovateli vytknu n, ve druhem jmenovateli  pokratim a v prvnim citateli bude
pokratim a v prvnim citateli bude  ve druhem
ve druhem 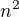 takze bych mel dostat
takze bych mel dostat 
dekuji
v pripade nejasnosti take napiste
Offline
#14 25. 11. 2010 21:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: analýza - limity posloupností
↑ myrek:
Zdravím,
tuto limitu jsem našla po letech a taková úprava se doporučovala - viz odkaz, hodně pěkně vysvětloval kolega Olin - viz odkaz, kolegovi děkuji.
Pomohlo? Děkuji.
Prosba pro celý tým řešitelů - jeden dotaz (tedy jedna limita) do tématu, nedá se v tom vyznat. Děkuji. Na původní zadání se můžete odkazovat.
Offline
#16 25. 11. 2010 22:40 — Editoval jelena (25. 11. 2010 22:40)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: analýza - limity posloupností
nejsem si úplně jistá, zda jsem správně pochopila rozšíření, ale řekla bych, že máme 2 různé vzorce - pro první zlomek 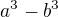 , pro druhy
, pro druhy  .
. ![kopírovat do textarea $\frac{(\sqrt[3]{n^3+3n^2}-n)+(n-\sqrt{n^2-n})}{sqrt{n}-\sqrt[3]{n}}=\frac{(\sqrt[3]{n^3+3n^2}-n)}{sqrt{n}-\sqrt[3]{n}}+\frac{(n-\sqrt{n^2-n})}{sqrt{n}-\sqrt[3]{n}}$](/mathtex/78/78b7757679cb203d60bf714f6e58c09d.gif)
Mám pocit, že v předloženém postupu je to "kombinováno". Tak?
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » analýza - limity posloupností (TOTO TÉMA JE VYŘEŠENÉ)

![kopírovat do textarea $\sqrt[n]{a^n}<\sqrt[n]{a^n+b^n+c^n}<\sqrt[n]{3a^n}=a\cdot\sqrt[n]{3}$](/mathtex/bd/bd597b498e4f00f8e948ad4856b18dc7.gif) , první a poslední mají stejné limity.
, první a poslední mají stejné limity.![kopírovat do textarea $\lim\sqrt[n]{n^3}=\lim\sqrt[n]{n}\cdot\lim\sqrt[n]{n}\cdot\lim\sqrt[n]{n}$](/mathtex/43/4379452d5adbdc2265f719f08a786da4.gif)
![kopírovat do textarea $\lim\sqrt[n]{5^n+n4^n-\[n^5\sin n\]}=5\cdot\lim\sqrt[n]{1+n\(\frac45\)^n-\frac{\[n^5\sin n\]}{5^n}}$](/mathtex/29/29c8730ca848a679bd4a3b2b72c602a8.gif)
![kopírovat do textarea $0<\|\frac{\[n^5\sin n\]}{5^n}\|<n\(\frac45\)^n<1$](/mathtex/2f/2f05621061352f2dbf6c16c94937ebd6.gif) a tedy
a tedy ![kopírovat do textarea $0<n\(\frac45\)^n-\frac{\[n^5\sin n\]}{5^n}<2$](/mathtex/b0/b0007cdf336a9b7cc8817e7b046f4d60.gif) .
. ![kopírovat do textarea $1\le\lim\sqrt[n]{1+n\(\frac45\)^n-\frac{\[n^5\sin n\]}{5^n}}\le\lim\sqrt[n]{3}=1$](/mathtex/c4/c4527d476d526d894eb115431af46bb6.gif) .
.
![kopírovat do textarea $\frac{(\sqrt[3]{n^3+3n^2}-n)+(n-\sqrt{n^2-n})}{sqrt{n}-\sqrt[3]{n}}=\frac{n^3+3n^2-n^3+n^2-n^2+n}{(sqrt{n}-\sqrt[3]{n})*((\sqrt[3]{n^3+3n^2})^2+(\sqrt[3]{n^3+3n^2})*n+n^2+n+\sqrt{n^2-n})} =$](/mathtex/28/28fe2225848daf9ea259ebde004e338f.gif)
![kopírovat do textarea $ =\frac{3n^2+n}{(sqrt{n}-\sqrt[3]{n})*(n^2*((\sqrt[3]{1+3/n^{neco}})^2+(\sqrt[3]{1/n^{neco}+3/n^{neco}})*1/n+1+1/n+\sqrt{1/n^{neco}-1/n^{neco}}))} =$](/mathtex/4b/4bbb08f0a91d9ca7ddab5b54ef88b9bf.gif)
![kopírovat do textarea $ =\frac{n^2*(3+\frac{1}{n})}{(sqrt{n}-\sqrt[3]{n})* n^2*((\sqrt[3]{1+3/n^{neco}})^2+(\sqrt[3]{1/n^{neco}+3/n^{neco}})*1/n+1+1/n+\sqrt{1/n^{neco}-1/n^{neco}})} =$](/mathtex/e1/e134ccf220507c6a163ef339364af3fd.gif)
![kopírovat do textarea $ = \frac{(3+\frac{1}{n})}{(sqrt{n}*(sqrt1-\sqrt[3]{1/n^{neco})})((\sqrt[3]{1+3/n^{neco}})^2+(\sqrt[3]{1/n^{neco}+3/n^{neco}})*1/n+1+1/n+\sqrt{1/n^{neco}-1/n^{neco}})} $](/mathtex/cd/cd776ca1a580fb8028373e0604cbab90.gif)
