Matematické Fórum

ttopi · 19. 06. 2008 07:16

↑↑ Cheop:
Ahoj, díky moc :-)
Vše je napsáno právě v této sekci :-)

kein.007 · 19. 06. 2008 22:06

V cestovnej kancelárii sú dvaja klienti. Prvý klient si zakúpi fakultatívny výlet s pravdepodobnos?ou p 1 = 0,7 a druhý klient s pravdepodobnos?ou
p2 = 0,4. Určte rozdelenie pravdepodobnosti zakúpenia fakultatívneho výletu dvomi klientmi .

velmi pekne vas prosim vypocitajte mi tento priklad,dakujem.surne
pls

jelena · 19. 06. 2008 22:36

↑ kein.007:

Myslim si, ze to bude tak :

Nahodna velicina - zakoupeni zajezdu muze nabyvat hodnot 0 (ani jeden nekoupi), 1 (jeden ano druhy ne), 2 (oba zakoupi)

P(X = 0) = (1-P(A))(1-(P(B)) = 0,3 * 0,6 (soucin pravdepod. opacnych jevu)

P(X = 1) = P(A) * (1- P(B)) + (1-P(A))* P(B) = 0,7 * 0,6 + 0,3 * 0,4

P(X = 2) = p(A) * P(B) = 0,7 * 0,4

Pak se sestavi takova tabulka

X 1 2 3
p P(X = 0) P(X = 1) P(X = 2) zde doplnit vypoctene hodnoty

Funkce rozdeleni (opet dopocitat]:

F(X) = 0 pro x mensi nebo rovno 0

F (x) = P(X = 0) pro x v intervalu (0,1>

F(x) = P(X = 0) + P(X = 1) pro x v intervalu (1, 2>

F(X) = P(X = 0) + P(X = 1) + P(X = 2) = 1 pro x vetsi 2

OK?

jelena · 19. 06. 2008 22:41

↑ kein.007:

Jeste toto mam snad dobre. A neco vyresil kolega ttopi

Na každom z troch úsekov A1, A2, A3 diaľnice v smere Prešov – Bratislava sú vykonávané dopravné kontroly. Pravdepodobnos? kontroly motorového vozidla je pre jednotlivé úseky rovná:P(A1)=0,7 P(A2)=0,8 P(A3) =0,9 . Aká je pravdepodobnos?, že motorové vozidlo bude kontrolované aspoň na dvoch úsekoch diaľnice

Bude kontrolováno alespon na dvou je jev opacny k kontrolovan nejvyse na jednom useku (moznosti – (není kontrola na zadnem useku) nebo (je kontrola na A1 nebo na A2 nebo na A3)

Pravdepodobnost jevu opacneho je:

P(A´ ) = (1- P(A1) ) *(1- P(A2)) * (1- P(A3)) + P(A1) * (1- P(A3)) *(1- P(A2)) + P(A2) * (1- P(A1)) *(1- P(A3)) + P(A3) * (1- P(A1)) *(1- P(A2))
= (1-0,7)*(1-0,8)(1-0,9) + 0,7*(1-0,8)*(1-0,9) +(1-0,7)*0,8*(1-0,9) + (1-0,7)*(1-0,8)*0,9 =
= 0,3*0,2*0,1 + 0,7*0,2*0,1 + 0,3*0,8*0,1 + 0,3*0,2*0,9

pravdepodobnost jevu P(A) = 1 - P(A´ )

↑ ttopi:

Zdravim :-)

priklad NOROVO urcite mas vice elegantne, nez ja. Ale kdyz ten nas kolega porad chtel vzorce, tak jsem to tam dala.

kein.007 · 23. 06. 2008 11:11

Na univerzite je 1000 počítačov pripojených k sieti Internet a na obrazovke 200 počítačov priemerne je natiahnutá univerzitná webová stránka. Pomocou asymptotických vzorcov určte pravdepodobnos?, že uvedená stránka je na obrazovkách 200 až 300 počítačov univerzity

chcem s vam velmi pekne podakovat a zaroven vas ziadam este o jedno riesenie prikladu vopred dakujem potreboval by som to este dnes ak by to slo

jelena · 23. 06. 2008 23:23 — Editoval jelena (24. 06. 2008 23:21)

↑ kein.007:

Zdravim :-)

Editace: odkaz na dobry material http://trial.kma.zcu.cz/Tdb/main.php?T0 … 7&C=./

to je jen navrh. Pravdepodobnost, ze na pocitaci je funkcni univerzitni stranka je 200/1000 = 0,2. Stranka "je nebo neni" - binomicke rozdeleni.
Aproximovat budeme normalovym rozdelenim (jelikoz p je vetsi jak 0,1 - proto neni aproximovano Poissonovym) a

n*p(1-p) =1000*0,2*0,8 = 160, coz je vic, jak 9 (podminka pro aproximaci normalovym)

$\mu=np=1000\cdot{0.2}=200$ a ${\sigma}^2=np(1-p)=1000\cdot{0.2}(1-0.2)=160$

$P(200{\leq}X{\leq300})=\phi\left(\frac{b-\mu}{\sigma}\right)-\phi\left(\frac{a-\mu}{\sigma}\right)= \phi\left(\frac{300-200}{12.65}\right) - \phi\left(\frac{200-200}{12.65}\right)$

$P(200{\leq}X{\leq300})=\phi\left(7.9\right) - \phi\left(0\right)=\phi\left(7.9\right) - 0.5$

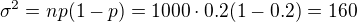
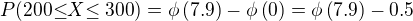
No, rada bych slysela nazor, zda to vubec ma hlavu a patu (alespon se snazim o upravu, kdyz vidim online Mariana, ktereho srdecne zdravim) :-)

Marian · 23. 06. 2008 23:42

↑ jelena:

Uprimne receno, jeleno, ja statistice nerozumim. Je sice zvykem v nasich luzich a hajich psat u desetinnych cisel tzv. desetinnou carku, ja se ovsem priklanim spise k desetinne tecce. Ale nechci odtahovat pozornost od statistiky. Ta diskuze by patrila jinam. Ja nemam vyhrady :-)

Ale dekuju za tvuj pozdrav. Take zdravim! Snad se "setkame" u nejake jine ulohy.

jelena · 23. 06. 2008 23:57

↑ Marian:

Jeste jednou zdravim :-) ja jsem prave tecky (psane na anglicke klavesnici) pred odeslanim prispevku opravila na carky, nebot jsem si nebyla jista zpusobem psani :-) ted uz vim.

Statistice bych rozumet mela, ale zjistila jsem, ze jsem nemela dobre zaklady v kombinatorice a ve zbytku mam docela problem si spravne priradit pojmy, ktere umim z rustiny. Potrebovala bych to jednou slyset :-) Tak usilovne cvicim a prezentuji tady svoji pokusy, ale statistika tady neni prilis popularni.

Z dnesnich uloh - netroufla jsem na toto, ale myslim, ze tam je dost chyb : http://forum.matweb.cz/viewtopic.php?id=3585 a take bych rada videla tvuj nazor na zaver tohoto prispevku http://forum.matweb.cz/viewtopic.php?id=3579 - ale treba i nekdy casem.

Hezky pozdrav a opravdu mam radost, kdyz se objevis online :-)

jelena · 04. 10. 2008 11:46

Zdravim kolegy a mam velkou prosbu :-)

Muzete, prosim, zkontrolovat moje vypocty v predchozich prispevcich tohoto tematu (u kombinatoriky a statistiky vzdy napisi, ze sobe nejak moc neverim, ale povinnosti pozaduji, abych to trochu lepe umela :-) Dekuji :-)

Matematické Fórum

#26 19. 06. 2008 07:16

Re: statistika a pravdepodobnost

#27 19. 06. 2008 22:06

Re: statistika a pravdepodobnost

#28 19. 06. 2008 22:36

Re: statistika a pravdepodobnost

#29 19. 06. 2008 22:41

Re: statistika a pravdepodobnost

#30 23. 06. 2008 11:11

Re: statistika a pravdepodobnost

#31 23. 06. 2008 23:23 — Editoval jelena (24. 06. 2008 23:21)

Re: statistika a pravdepodobnost

#32 23. 06. 2008 23:42

Re: statistika a pravdepodobnost

#33 23. 06. 2008 23:57

Re: statistika a pravdepodobnost

#34 04. 10. 2008 11:46

Re: statistika a pravdepodobnost