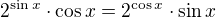Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 23. 08. 2014 11:40
Offline
#4 23. 08. 2014 12:24
#9 23. 08. 2014 12:56
- janina.kucera
- Příspěvky: 38
- Reputace: 0
Re: rovnice
↑ duskin: to právě vím, že tento postup nejde, ale nevím, jak jinak ronici řešit. Nějaké další návrhy?
Offline
#12 24. 08. 2014 10:49
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: rovnice
Zdravím,
↑ Sherlock:
kolega Sherlock napsal(a):
Z grafu jsem si všiml, že řešení té rovnice budou takové body...
Toto je vhodné vodítko k řešení, ale graf není důkaz, jak víme a je nám opakováno :-). Sice i bez nástrojů (jen s vlastnosti funkcí) můžeme pracovat s grafy  a
a  a s jejich součtem a (snad i) dokázat, že minima odpovídají minimům pro funkci
a s jejich součtem a (snad i) dokázat, že minima odpovídají minimům pro funkci 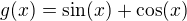 - což sice usnadní postup hledání. Ale neprokážeme takto, že je to řešení jediné (s ohledem na periodičnost funkce teď mluvím o "jediném řešení na základním intervalu", ať to není matoucí). Souhlasíš?
- což sice usnadní postup hledání. Ale neprokážeme takto, že je to řešení jediné (s ohledem na periodičnost funkce teď mluvím o "jediném řešení na základním intervalu", ať to není matoucí). Souhlasíš?
↑ janina.kucera:
odkud je úloha a jaké nástroje předpokládá k použití. Překlep v zadání bych zde spíš vyloučila, jelikož ten výsledek je viditelný, ale není mi zatím patrná cesta k výsledku. Děkuji za upřesnění.
Offline
#13 24. 08. 2014 11:08 — Editoval Xellos (24. 08. 2014 11:12)
Re: rovnice
Pouzime AG nerovnost: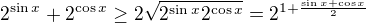
Z monotonie  staci dokazat, ze
staci dokazat, ze 
a zistit, kedy nastava rovnost (len to potom mozu byt riesenia povodnej rovnice). Urcite su aj ine metody, ale mne pride najlahsie zderivovat a hladat extremy: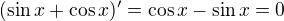
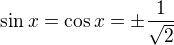
z coho to uz vidno. Dostavame ako riesenie 1 bod na 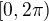 , ktory vidime ze riesi povodnu rovnicu.
, ktory vidime ze riesi povodnu rovnicu.
Offline
#14 26. 08. 2014 20:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: rovnice
↑ Xellos:
Zdravím a děkuji za nástin důkazu, škoda, že kolegyně ↑ janina.kucera: zatím nedoplnila zdroj zadání a povolené nástroje.
Offline
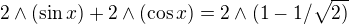

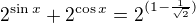

 , takže
, takže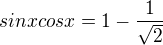

 nabývá minima. K určení takových bodů je třeba řešit rovnici:
nabývá minima. K určení takových bodů je třeba řešit rovnici: