Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 07. 2009 20:49 — Editoval simonaj1 (15. 07. 2009 21:01)
x=e^x
tak mám další dotaz jak mám tohle zlogaritmovat, bych dostala hodnotu x  měl by to být jeden z kořenů první derivaci při vyšetřování fce
měl by to být jeden z kořenů první derivaci při vyšetřování fce 
už jsem na to asi přišla, tenhle kořen neexistuje, protože neexistuje řešení v oboru R čísel.... je to tak?
Offline
#2 15. 07. 2009 21:17
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: x=e^x
↑ simonaj1:
Zdravím,
ano,  kořen neexistuje, stačí si nakreslit graf funkcí
kořen neexistuje, stačí si nakreslit graf funkcí  a
a  a zkontrolovat průsečík (není).
a zkontrolovat průsečík (není).
Ovšem to nijak nesouvisí s vyšetřením zadané funkce: 1. derivace funkce  bude mít v čitateli (1-x), pokud máš na mysli, pro které x je derivace nulová.
bude mít v čitateli (1-x), pokud máš na mysli, pro které x je derivace nulová.
OK?
Offline
#4 15. 07. 2009 21:37
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: x=e^x
↑ simonaj1:
odkud se vzal v 1. derivaci 2. kořen (nějak mi to uniká)?
asymptota by měla vycházet y=0.
Vzorce pro asymptoty máš dobře?
Doučování určitě pomůže, také toho hodně děláš samostatně, obdivuji - ať se daří.
Offline
#6 15. 07. 2009 22:12
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: x=e^x
↑ simonaj1:
rozumím, děkuji.
Offline
#7 15. 07. 2009 22:23
Re: x=e^x
↑ jelena: jj, jen je to docela drahé a docela daleko na dojíždění, málokdo tady v okolí dělá doučování VŠ matiky, takže se musím snažit sama a jezdím na doučko jen s tím co mi nejde... bez vás bych byla nahraná, vy všichni jste to nejlepší doučování na světě;-)
moc vám všem díky, zkoušku mám na začátku září, schválně jsem si to nechala nakonec, abych to zvládla přes prázdniny dát nějak dohromady, tak snad se podaří...
Offline
#8 16. 07. 2009 20:34
Re: x=e^x
↑ jelena:
Jeleno, není možné zdůvodňovat neřešitelnost jisté rovnice v jisté množině náčrtkem. Jako vždy to myslíš ale dobře.
Otázka pro jelenu (popř. i pro ostatní). Víš, jak se dokáže, že neexistuje řešení rovnice  v oboru reálných čísel? (Nápověda: Stačí k tomu matematika z průmyslovky.)
v oboru reálných čísel? (Nápověda: Stačí k tomu matematika z průmyslovky.)
Zdravím ...
:-)
Offline
#9 16. 07. 2009 21:23
Offline
#10 17. 07. 2009 21:58
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: x=e^x
↑ Marian:
Zdravím, Mariane,
již jednou jsem byla napomínana - Tvůj příspěvek č. 8, že nemohu používat obrázek jako důkaz neexistence řešení.
Bohužel neumím žádný důkaz, který by nebyl postaven na vlastnostech funkcí a na moji představě o grafech těchto funkci, což určitě není to pravé, co má být. Navíc, já bych nedokazala žádný matematický důkaz formulovat v takové formě, aby to nepůsobilo komicky.
Jedinou oblast důkazů, kterou snad trochu umím, jsou geometrické důkazy a i tam už bych dost váhala.
Původně, po přečtení Tvé připomínky jsem přemyšlela, zda z toho nemám vyvodit závěr zcela jiného rázu, a to zda vůběc mám mít tu troufalost sem umísťovat své příspěvky. Ale..."byla by tu riadna nuda"(c).
Vážně - Tvého vyjádření k mé tvorbě si velmi vážím a opravdu je mi lito, že jsem to první upozornění nějak nepozorně přešla - tak se ptám, jak to má správně být?
Rozumím tomu tak, že i grafickému řešení, které já všude upřednostňuji, má předcházet diskuse o počtu řešení nebo neexistenci. To nepovídá ani váš Polák, ani náš Skanavi, nebo jsem to špatně četla.
Pro Simonu,
zdravím a děkuji za pochvaly, doufám, že to se dostalo hlavně ke čtení kolegům, kdo se tento rok podílí na přípravě na zkoušku. Já moc ne - jelikož jsem se na stejné sbírce od stejného učitele již se podílela v minulém roce:
http://www.google.cz/search?q=site:matw … 0&sa=N
http://www.google.cz/search?q=site:matweb.cz%20bons
ale snad budu užitečna, pokud budeš mít dotazy z technologie, z chemie nebo z něčeho podobného, čemu trochu rozumím (to je úkazka snad jediného příspěvku, kdy opravdu rozumím jak teoreticky, tak i prakticky).
-----------------------
Астрономы нашли в космосе оранжево-зелено-фиолетовую дыру. Она так же загадочная и опасная, как и черная, но смотреть на нее значительно веселей.
Offline
#11 19. 07. 2009 09:23
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: x=e^x
↑ Marian:
Berou průmyslováci derivace? Použil bych řešení podobné ↑ jelena:.
Jednoduše si rozdělím Df na 3 části, R-, 0 a R+.
V R- je vidět, že 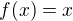 bude nabývat záporných hodnot, zatímco
bude nabývat záporných hodnot, zatímco  hodnot kladných. V nule máme funkční hodnoty 0 a 1. Teď si spočítáme derivace.
hodnot kladných. V nule máme funkční hodnoty 0 a 1. Teď si spočítáme derivace.  ,
,  . Jelikož jsme v Dg "za" nulou, můžeme dát do nerovnosti
. Jelikož jsme v Dg "za" nulou, můžeme dát do nerovnosti  . Víme tedy, že exponenciála má vždy (na této části Dg) větší derivaci a tím pádem i větší strmost, takže se s
. Víme tedy, že exponenciála má vždy (na této části Dg) větší derivaci a tím pádem i větší strmost, takže se s  nikdy neprotne.
nikdy neprotne.
---
Graficky, za pomocí nějaké té matematiky. Může být?
Offline
#12 19. 07. 2009 14:05 — Editoval jelena (19. 07. 2009 14:06)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: x=e^x
↑ halogan:
Zdravím a děkuji za reakci,
nevím, zda průmyslovka derivuje (mistní gymnázium má dif. a int. počet pouze v semináři), spíše si myslím, že se očekává povídání, že po úpravě máme funkci  , která je definována a spojitá na R a nedochází ke změně znaménka hodnoty funkce na R, tedy není řešení rovnice
, která je definována a spojitá na R a nedochází ke změně znaménka hodnoty funkce na R, tedy není řešení rovnice  .
.
Ale funkce f(x)=x a g(x)=e^x jsou snad natolik jasné, co do grafického náčrtku, že bych zde nehledala nějaké závažnější zdůvodnění.
U některých "trochu složitějších" rovnic bych si možna něco vymyšlela, jaké zdůvodnění se hodí pro numerické zjištění řešení rovnic, ale stejně bych zůstavala u grafu (buď pomocí "rychlého vyšetření průběhu" nebo jak tady předvádím zcela zbytečný nácvik ručního kreslení grafu).
Tak se budeme těšít na precizní vysvětlení Mariana, snad na to bude mít náladu a čas, děkuji.
Offline
#13 19. 07. 2009 21:40
Re: x=e^x
↑ jelena:↑ halogan:
Bral jsem to ze svého pohledu. Jako absolvent průmyslovky v oboru automatizace jsem derivoval v 16-i. Myslel jsem na derivace. Nepřipouštěl jsem si elementárnější důkaz, protože každý takový krok tímto směrem může přinést nežádoucí těžkopádnost budované úvahy. Tuším, že ne každý středoškolák je schopen říci precizně, co to je exponenciální funkce, tj. exp(x). Problém je v tom, že není kdy, popř. jak, precizně zdůvodnit na SŠ širšímu žactvu, co to je Eulerovo číslo.
Nemínil jsem poznámku jeleně nijak zle. Někdy musíte mé poznámky přečíst s úsměvem a nebrát si je příliš vážně.
Všechny Vás zdravím ...
Offline
#14 20. 07. 2009 00:57
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: x=e^x
↑ Marian:
Mariane, zdravím srdečně a děkuji za vyjasnění problému,
Marian napsal(a):
Někdy musíte mé poznámky přečíst s úsměvem a nebrát si je příliš vážně.
Tvé (a nejen Tvé, ale i poznámky dalších kolegů) obvykle pročitám s usměvem a alespoň se snažím brát přiměřeně vážně (což mi zas až tak moc nejde). Doufám také, že máme dostatečný nádhled a rozumíme, co je skutečně podstatné.
Derivovat v 16-i je snad normální - jako absolventka střední všeobecně vzdělavací školy také tuto zkušenost mám, ale my jsme měli výuku i v sobotu (i na VŠ také v sobotu) a co je dnes komu těžké vysvětlovat - to je na dlouhé OT, tak ani nezačnu.
Pozdrav :-)
Offline
#15 20. 07. 2009 09:25 — Editoval musixx (20. 07. 2009 09:58)
Re: x=e^x
Tohle vlákno mě motivovalo k úloze, pro jaké (kladné)  je přímka
je přímka 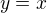 tečnou k exponenciále
tečnou k exponenciále  . Je to na pohled zajímavé, vyjde
. Je to na pohled zajímavé, vyjde![kopírovat do textarea $a=\sqrt[\mathrm{e}]{\mathrm{e}}\dot=1.444668$](/mathtex/e2/e2929c9d1d5663493ed6e90c892b09e0.gif) .
.
Kdyby byl zájem, můžu doplnit výpočet, ale není to vlastně nic moc složitého (stačí uvážit fakt, že takové  existuje, a umět třeba trochu logaritmovat, případně hledat (kladné)
existuje, a umět třeba trochu logaritmovat, případně hledat (kladné)  přímo ve tvaru
přímo ve tvaru  , jak se to ostatně občas vyplatí i jinde).
, jak se to ostatně občas vyplatí i jinde).
Offline
#16 20. 07. 2009 12:50 — Editoval Rumburak (20. 07. 2009 13:20)
Re: x=e^x
↑ jelena:
Ahoj Jeleno, "důkazy" pomocí obrázků nejsou považovány za korektní zejména proto, že mohou být zavádějící.
Například existuje reálná funkce, která je SPOJITÁ na daném intervalu I, přitom ale její graf v žádném svém bodě nemá tečnu
(neboli funkce nemá v žádném bodě intervalu I derivaci). Taková funkce rovněž v žádném intervalu, který je částí intervalu I,
není monotonní.
Funkci s těmito vlastnostmi je obtížné si představit, natož ji nakreslit a nikomu se to ještě nepodařilo, takže bychom se
mylně mohli domnívat, že neexistuje.
Proto každý názor plynoucí z obrázku je nutno brát s reservou a nelze mu přisuzovat platnost důkazu.
Offline
#17 20. 07. 2009 13:18 — Editoval jelena (20. 07. 2009 13:21)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: x=e^x
↑ Rumburak:
Zdravím,
já nenabízím obrázky (grafy) jako řešení každého problému, ani jako důkaz - povídám, že důkazy ani neumím "slušně" matematicky formulovat. A už jsem všechno pochopila z výkladu Mariana, sdělení kolegy Rumburaka také pozorně prostuduji.
Ale v rovině mat. analýzy pro bc. obory technických VŠ je to docela slušná pomůcka minimálně pro odhad, jak asi funkce vypadá. Kdyby naše kolegyně Simona uměla tento odhad provést pro své zadání, které řeší tady:
http://forum.matweb.cz/viewtopic.php?pid=64397#p64397 tak by věděla, že grafy  a
a 
maji 2 společné body, tedy budou 2 průsečíky s osou x a asi kde budou (mezi 0 a 1 a "kousek" po 1) - a že se to počítá jen přibližně atd.
Ale já už tam do toho tématu teď vstupovat nebudu, čas bych stejně měla až tak věčer, ale, pokud mohu moc poprosit, udělejete si alespoň jasno, které zadání Simona řeší.
A neokouzlujte Simonu Lambertovou funkci - takové hezké úvodní přivítání mám pro kolegu Kondra - zdravím ale opravdu velmi srdečně :-)
Také se zaměřte na úlohu, která se tady v tématu ztrací - od kolegy musixx, kterého také moc zdravím.
A už jsem vychovavala dost - zdravím, koho jsem ještě dnes nezdravila, a už se loučím.
konec OT.
Edit: ještě vidím online lukaszhe a také moc zdravím :-)
Offline
#18 20. 07. 2009 13:29
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: x=e^x
↑ jelena:
Osobně to beru takhle: radši ať člověk ví, jak to vypadá, i když to má nepřesně, než když to spočítá numericky úplně blbě (a neví, která bije).
Stejně jako jelena neberu grafický náčrt jako jakoukoliv formu důkazu, ale jako vodítko a pomoc při řešení.
Offline

 takže jsem položila
takže jsem položila  no a pak
no a pak  pak mi došlo, že je to nereálné protože je to vlastně
pak mi došlo, že je to nereálné protože je to vlastně  tudíž 1=0 a to je nesmysl...
tudíž 1=0 a to je nesmysl... je derivovaťeľná v R teda aj spojitá v R a jej derivácia je
je derivovaťeľná v R teda aj spojitá v R a jej derivácia je má záporné hodnoty pre záporné x a kladné pre kladné x funkkcia f je teda klesajúca na záporných a rastúca na kladných číslach a naviac spojitá v nule preto má v nule globálne minimum ktoré je však rovné číslu
má záporné hodnoty pre záporné x a kladné pre kladné x funkkcia f je teda klesajúca na záporných a rastúca na kladných číslach a naviac spojitá v nule preto má v nule globálne minimum ktoré je však rovné číslu  teda globálne minimum fcie je kladné teda sú všetky hodnoty fcie kladné máme teda nerovnosť
teda globálne minimum fcie je kladné teda sú všetky hodnoty fcie kladné máme teda nerovnosť  z toho priamo vyplýva
z toho priamo vyplýva  teda e^x sa nerovná x
teda e^x sa nerovná x