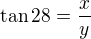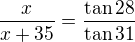Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 05. 2010 14:58
Matika v praxi
Ahojte mohli byste mi pomoct jen s nákresem obrázku?nějak jsem to nepochopil díky
Zadání:
Na vrcholu kopce stojí rozhledna 35 vysoká,patu i vrchol vidíme z určitého místa v údolí pod výškovými úhly o velikosti alfa=28°,beta=31°.Jak vysoko je vrchol kopce nad rovinou pozorovacího místa?
Toto mě napadlo:
Offline
- (téma jako vyřešené označil(a) jelena)
#2 03. 05. 2010 15:00 — Editoval frank_horrigan (03. 05. 2010 15:04)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Matika v praxi
Aplikovanou matiku zavánějící geodézii miluju. Ten náčrtek máš dobře, ale ty úhly máš špatně.... máš VÝŠKOVÝ, tedy od horizontální roviny vztaženy
Rozdíl těch úhlů máš 3°... a tyhle 3°ti dělají 35 metrů. kolik metrů ti bude dělat úhel alfa (tedy vrchol kopce od pozorovací roviny)?
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#4 03. 05. 2010 15:16 — Editoval frank_horrigan (03. 05. 2010 15:17)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Matika v praxi
↑ VitKovar:
Uhly ti vysvetlim, pak najdu, kde jsem udelal chybu... Výškový/hloubkový úhel je takový úhel, který začíná na horizonální rovině, která prochází osou stroje, kterým ty úhly měříš. Proste kdyz koukáš vodorovně dopředu, výškový úhel je nula, a zvedá se čím koukáš výš. Ovšem se nemění ta 0. Takže kdyz patu vidíš pod úhlem 28°, vrchol 31°, tak to je pořád ten úhel vztažený k té horizontále. Není to tak dávno, co jsem to tady vysvetloval, ten thread ti najdu.... jo, a uz vim, kde je chyba - to je tak, kdyz delám pět vecí zároven.. ten přírustek je samozřejmě nelineární, ale sinusoidní - tedy sin 3° = 35m , sin 28° = x metru, dopočítej x :)
EDIT: tady se to nedávno řešilo :) http://forum.matweb.cz/viewtopic.php?id=17443
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#5 03. 05. 2010 15:18
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Matika v praxi
↑ frank_horrigan:
Trojčlenkou na to jít nemůžeme.
↑ VitKovar:
Jak jste si zaváděli tangens?
Nakresli si nový obrázek, tentokrát správný a výpočty budou takové: ,
,
kde  je výška kopce a
je výška kopce a  je vzdálenost od toho kopce (a ta nás nezajímá, takže si ji vyjádříme).
je vzdálenost od toho kopce (a ta nás nezajímá, takže si ji vyjádříme).
Offline
#7 03. 05. 2010 15:25
Offline