Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 10. 2010 20:14
- check_drummer

- Příspěvky: 4900
- Reputace: 105
Neceločíselný výraz
Nedávno jsem viděl tuším v sekci VŠ tuto úlohu, myslím, že by mohla být označena jako zajímavá:
Dokažte nebo vyvraťe, že  není přirozené číslo pro všechna n>1.
není přirozené číslo pro všechna n>1.
"Máte úhel beta." "No to nemám."
Offline
- (téma jako vyřešené označil(a) check_drummer)
#3 22. 10. 2010 08:17
Re: Neceločíselný výraz
↑ check_drummer:
Úloha je poměrně známá a tak uvedu pouze zajímavý materiál (sekce 4), kde se dají najít zajímavá tvrzení o harmonické řadě (PDF).
Nikomu ovšem nechci brát chuť na řešení. Můj příspěvek tedy lze dle uvážení ignorovat.
Offline
#7 25. 10. 2010 19:01
Re: Neceločíselný výraz
↑ Honzc:
Nechť  je libovolné přírozené číslo. Kde bereš tu jistotu, že nemůže nastat pro nějaké přirozené
je libovolné přírozené číslo. Kde bereš tu jistotu, že nemůže nastat pro nějaké přirozené  rovnost
rovnost
když o číslu  nevíš téměř nic? Připomínám, že
nevíš téměř nic? Připomínám, že  a
a  jsou na sobě nezávislá čísla.
jsou na sobě nezávislá čísla.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#9 26. 10. 2010 09:50 — Editoval Pavel (26. 10. 2010 09:51)
Re: Neceločíselný výraz
↑ Honzc:
To máš sice pravdu, nicméně to neřeší problém, proč by nemohla nastat situace, že  , kde m, n jsou výše uvedená přirozená čísla. K(n) závisí na n - s měnícím se n se mění také K(n). Proč by součet dvou iracionálních čísel nemohl být celé číslo
, kde m, n jsou výše uvedená přirozená čísla. K(n) závisí na n - s měnícím se n se mění také K(n). Proč by součet dvou iracionálních čísel nemohl být celé číslo  ?
?
Jak vlastně definuješ číslo doplňkové? Vztah 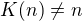 otázku případné rovnosti
otázku případné rovnosti  neřeší. Je totiž třeba ukázat, že takové m neexistuje, ať je n libovolné přirozené číslo.
neřeší. Je totiž třeba ukázat, že takové m neexistuje, ať je n libovolné přirozené číslo.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline


