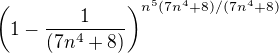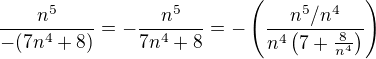Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » limita s exponentom (TOTO TÉMA JE VYŘEŠENÉ)
#3 06. 11. 2010 14:48
Re: limita s exponentom
zdravim !
podarilo sa mi to upravit na ( 1 - 1/ 7nnnn + 8 ) a to cele na 7nnnn+1 + nnnnn/7nnnn+8
ale problem je ze v zatvorke ostal rozdiel a neviem ci vobec tato uprava dokaze pomoct na prevod limity e
DIK moc za ujasnenie, dufam ze ste to vylustili tie n :)
Offline
#4 06. 11. 2010 17:40
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limita s exponentom
Zdravím, zejména kolega Lukáš má smysl pro nápaditost úpravy a lingvistiku. Závorku nějak tak bych si představila: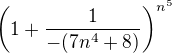
vysoka napsal(a):
dufam ze ste to vylustili tie n :)
a to cele na 7nnnn+1 + nnnnn/7nnnn+8
nemám slovník, bohužel toto jsem nepřeložila, zkus sam(a) pomoci návodu na matematický zápis, jak je uvedeno v pravidlech nebo nad oknem zprávy.
Asi bude potřeba nějakých podobných úprav pro dosažení 2. pozoruhodné limity. Děkuji.
Offline
#6 06. 11. 2010 21:19
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limita s exponentom
↑ vysoka: děkuji, podařilo se to tedy poupravovat podle vzoru v odkazu?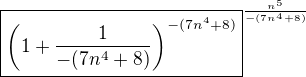
v krabičce je to, co se vztahuje k e, zbytek úprav a formální zápis podle vzoru v odkazu (až na hranaté závorky).
-------------------
minulý týden mi ukazali ještě jednu úpravu pro tuto limitu (pomoci substituce), ale byl to velký kulturní šok, tak se zatím nepodělím.
Offline
#8 06. 11. 2010 23:35
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limita s exponentom
↑ vysoka:
to bych neřekla, že výsledek je ![kopírovat do textarea $\sqrt[7]{e}$](/mathtex/cb/cbf980dc3b6e56e2cfa8cf7ace46fa23.gif) . Pomocí kterých úprav v exponentu (nad krabičkou)
. Pomocí kterých úprav v exponentu (nad krabičkou) 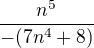 jsi šel k výsledku?
jsi šel k výsledku?
Jinak výsledek se dá překontrolovat i pomocí online nástrojů v úvodním tématu VŠ.
Offline
#10 07. 11. 2010 14:27
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limita s exponentom
↑ vysoka: prosím, pokud je problém používat v tématech VŠ zápis v místním TeX, nebyla by možnost alespoň používat závorky? Děkuji.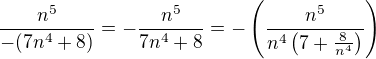
Může být? Děkuji.
Offline
#13 07. 11. 2010 16:27
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limita s exponentom
odstraniš ho tak, že ho vymažeš (chceš poradit postup, jak se maže?)
tak jsi to myslel? 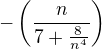 a potřebujeme zjistit limitu pro n k nekonečnu. Už se podaří? Děkuji.
a potřebujeme zjistit limitu pro n k nekonečnu. Už se podaří? Děkuji.
Offline
#17 07. 11. 2010 17:13
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limita s exponentom
↑ vysoka:
ano, celý exponent nad e je to "minus nekonečno".
Spíš, než wolfram, nám pomuže fakt, že 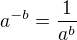 za platných podmínek pro a, b.
za platných podmínek pro a, b.
----------
"aj tie online nastroje su fajn ...nie vzdy , ale tiez zabehu hodne casu ked kym to tam clovek zada" (c)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » limita s exponentom (TOTO TÉMA JE VYŘEŠENÉ)