Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 12. 2010 20:27
prubeh funkcie
zdravim ked vidim tiet okrkolomne odpovede tak ma aj presla chut pocitat ... vedeli by ste niekto poradit ako sa najrychlejsie dopatrat k vysledku, resp nejaky fajn program na webe na ujasnenie ... ? Diky
vo wolframe som skusil, ale neviem .... v otazke sa pise o lokalnom maxime a pravda je ze je tam lokalnyh maxim nekonecne vela takze skor globalne maximum ...
Offline
- (téma jako vyřešené označil(a) vysoka)
#2 10. 12. 2010 20:30
Re: prubeh funkcie
http://www3.wolframalpha.com/input/?i=y … +x+%2B2%29 vsak posudte sami ...
Offline
#3 10. 12. 2010 23:36
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: prubeh funkcie
vysoka napsal(a):
http://www3.wolframalpha.com/input/?i=y%3D%28sinx+%2B1%29+%2F+%28cos+x+%2B2%29 vsak posudte sami ...
Máš pravdu - Айвазовский to není.
Jak vidíš sám na obrázku (z Wolframu) funkce má hodně lokálních extrému (maximů a minimů) periodicky opakujících se. O globálním extrému by se dálo povídat v případě vymezení nějakého konkrétního intervalu - překontroluj si definice lokálního a globálního extrému).
Pokud bys měl možnost používat Wolfram, tak bys překontroloval hodnoty funkce v jednotlivých bodech x=... a potom by se dalo rozhodnout, v kterých platí tvrzení. Zkus to tedy projit postupně s obrázkem (první hodnotu funkce můžeme vyločit rovnou - proč?)
Jelikož se mi nezdá, že bych pohotově dokázala si představit graf funkce jeko podíl funkcí "čitatel"/"jmenovatel", derivovala jsem jako podíl a položila jsem výsledek derivování (pouze čitatel) rovný nule.
Tak jsem zjistila body podezřelé z extrémů - což mohu porovnat s nabídkou výsledků v testu.
Třeba od kolegů bude lepší nápad.
A neodpovídej si, prosím, sam (lepší EDIT původního příspěvku). Potom se takové téma zatoulá.
Offline
#5 12. 12. 2010 13:25
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: prubeh funkcie
↑ vysoka: děkuji, ale bohužel tomuto Tvému zdůvodnění nerozumím.
Zkusím ještě jednou návodnou otázku - proč rychle vyloučíme odpověď e) - bez použití grafu z Wolfram, jen ze zadání funkce.
To jsou jen doporučení, jak pracovat se zadáním testu - hodí se pro případnou kontrolu. Ale asi neúčinné, nebo neumím vysvětlovat.
------------------
Jinak asi zvolit klasiku - derivovat a položit výsledek derivace rovný 0. To se podařilo? Děkuji.
Offline
#9 12. 12. 2010 20:50
#11 12. 12. 2010 23:19
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: prubeh funkcie
↑ vysoka: a máš v plánu řešit? Nebo se jen postěžovat?
Mně vyšlo v čitateli 1. derivace: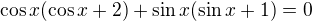 po úpravě:
po úpravě: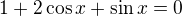 ↑ použila jsem:
↑ použila jsem: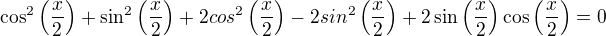
po úpravách jsem všechno vydělila 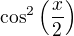 (neekvivalentní úprava, překontrolovat), ale lepší úpravu jsem nevymaslela. Měla jsem řešitelnou kvadratickou rovnici, kterou jsem ovšem dál neřešila.
(neekvivalentní úprava, překontrolovat), ale lepší úpravu jsem nevymaslela. Měla jsem řešitelnou kvadratickou rovnici, kterou jsem ovšem dál neřešila.
A Tobě vyšlo co? Děkuji.
Offline
#13 15. 12. 2010 14:31
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: prubeh funkcie
↑ vysoka:
tedy máš v plánu se jen postěžovat :-)
Máme možnosti:
- dořešit rovnici, co jsem navrhla ↑ jelena:, nebo
- do zápisu 1. derivace dosazovat hodnoty x=... ze zadání a sledovat, pro kterou x je 1. derivace nulová. Potom ověřit, zda je to max nebo min.
Chybí nám ovšem 3. cesta...
Offline
#15 15. 12. 2010 22:09
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: prubeh funkcie
↑ vysoka:
V zadání máš zápis funkce - to je tá čast, kde je sin a cos. A potom nabídku tvrzení pro různá x.
Ověřujeme, které tvrzení je platné, tedy můžeme používat všech údajů, co máme v zadání (i včetně tvrzení). Něco jsme vyloučili už přímo ověřením hodnoty funkce v bodech a, e,
Pro body b, c, d (případně f) nabízím:
- hledat stacionární body pomocí 1. derivace (kde je nulová). Buť dořešením rovnice 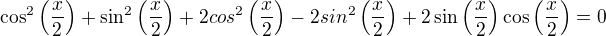
nebo
- dosazováním x=(7/2)pi nebo x=(3/2)pi nebo x=pi-arctg(3/4) do výrazu pro 1. derivaci 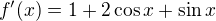 a sledovat, kde je nulová.
a sledovat, kde je nulová.
Žádný jiný nápad rychleho odvození max nebo min podílu funkce (sin(x)+1) a funkce (cos(x)+2) jsem nevymyslila.
Offline
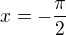 ) priratane +1 resp +2 tak to je ocividne ze to nebude odpoved e (skoro (c)).
) priratane +1 resp +2 tak to je ocividne ze to nebude odpoved e (skoro (c)).