Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Sestrojit trojuhelník v kružnici, aby měl co největší obsah (TOTO TÉMA JE VYŘEŠENÉ)
#26 02. 03. 2011 11:19
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
↑↑ Honzc:
Zdravím a děkuji za další řešení.
Vážený bratr to již vyřešil v příspěvku 14 ↑↑ Cheop:. Ovšem po mém staršesesterském upozornění ohledně poskytnutí kompletních řešení své řešení schoval do hide.
"Problém" autora dotazu je v tom, že to s nim nikdo nechce projit krokově a pořád se mu nabizí celé řešení. Když jsem se o to pokoušela se spolužákem autora dotazu, tak už se mi neozval.
Starší sestry jsou neuvěřitelně nudné osoby.
Offline
#27 02. 03. 2011 14:59
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
Já bych řekl, že už to vyřešené bylo ne? Nakreslil jsem si to znova a zkoušel jsem si to vypočítat sám:
1) hledaná přímka bude mít rovnici y=-m
2)obsah trojuh. je S=z*v/2
3)spočítáme si neznámé tj základnu a výšku. Základna se spočítá z trojuhelníku n/2=sqrt(a^2-m^2). /* Zde se chci zeptat, proč je přepona "a" označena jako přímka "a" od bodu "S". */ Výšku si spočítáme v=m+a.
4)dosadíme do vzorečku pro obsah. Vykrátíme, upravíme. /*Zde bych měl dotaz když: s^2=a^4+2a^3m-2am^3-m^4 zderivujeme podle m a položíme 0. Tak derivace je směrnice tečny. Derivací podle m získáme co? A ještě proč se to pokládá 0? Jinak zderivoval jsem úspěšně podle m*/
5)/*Proč se ověřují ty podmínky k 0? (a+m)^2=0 výjde a=-m tzn. že pokud bych to dosadil do rovnice pro přímku vyšlo by y=--m ale ten bod nemůže být logicky v kladných hodnotách od bodu S. Lze si to takhle zdůvodnit? (2m-a)=0 vyšlo že m je polovina a, což by mohlo odpovídat*/
6)dosadíme do rovnice přímky y=-a/2
7)dosadíme do Smax=z*v/2 ; základna: 2sqrt(a^2 - (a/2)^2 ) ; výška: a+a/2 a vypočteme Smax
/*...*/ jsem vyznačil jako otázky k příkladu
Offline
#28 02. 03. 2011 15:23
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
Předně se omlouvám, že do tohoto tématu pořád zasahuji a děkuji kolegům za řešení a nápovědy.
↑ Tomaskocz:
Děkuji, přesně tak si představuji spolupráci, o kterou prosím jak autory dotazů, tak kolegy, co poskytuji odpověď.
spočítáme si neznámé tj základnu a výšku. Základna se spočítá z trojuhelníku n/2=sqrt(a^2-m^2).
/* Zde se chci zeptat, proč je přepona "a" označena jako přímka "a" od bodu "S". */
Ze středu S do každého bodu na kružnici je stejná vzdálenost rovna poloměru kružnice (délka úsečky a=poloměr).
4)dosadíme do vzorečku pro obsah. Vykrátíme, upravíme.
/*Zde bych měl dotaz když: s^2=a^4+2a^3m-2am^3-m^4 zderivujeme podle m a položíme 0. Tak derivace je směrnice tečny. Derivací podle m získáme co? A ještě proč se to pokládá 0? Jinak zderivoval jsem úspěšně podle m*/
 je neznámá (lépe by bylo označit jako
je neznámá (lépe by bylo označit jako  , bylo by více průhledné).
, bylo by více průhledné).
Sestavili jsme funkci 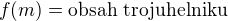 a hledáme extrém takové funkce.
a hledáme extrém takové funkce.
Jeden ze způsobu nalezení extrému je hledaní takových bodů, ve kterých 1. derivace je nulová + ověření, zda skutečně je extrém.
Geometrický význam derivace je směrnice tečny - ano. Nulová derivace značí, že směrnice je nulová, tedy tečná je rovnoběžná ose x. V bodech extrému tomu tak bude.
5)/*Proč se ověřují ty podmínky k 0? (a+m)^2=0 výjde a=-m tzn. že pokud bych to dosadil do rovnice pro přímku vyšlo by y=--m ale ten bod nemůže být logicky v kladných hodnotách od bodu S. Lze si to takhle zdůvodnit? (2m-a)=0 vyšlo že m je polovina a, což by mohlo odpovídat*/
Podmínky ověřujeme z důvodů:
- je zadaná konkretní situace (mezi hodnotou parametru a a nalezenou hodnotou m je určitý vztah ze zadání,
- při řešení provádíme umocnění (neekvivalentní úprava), našli jsme více řešení.
Závěr, že sečná nesmí být totočna s tečnou procházející bodem A, jinak místo troúhelníku bude jen jeden bod se mi zdá v pořádku.
Doporučuji ještě více podrobně si prostudovat užití derivace funkce pro vyšetření extrému funkce. Měli bychom ještě provést ověření, zda v nalezeném bodě (podezřelém z extrému) skutečně extrém nastává.
Stačí tak na úvod? Pokud jsem něco přehledla, upřesní, prosím. Děkuji.
Offline
#29 02. 03. 2011 15:35
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
No já si myslím, že tohle je úplně super formulace a vysvětlení :-) Jinak s tím kolegou ghostm, to řešíme spolu je to spolužák. Nemohli jsme na to přijít, hledali jsme na netu a nic jsme dokupy nedali.
Děkujeme
Offline
#30 03. 03. 2011 09:40
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
↑ Tomaskocz:
To "a"j e tam proto, že je to poloměr kružnice: 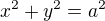 - ze zadání
- ze zadání
Nikdo není dokonalý
Offline
#32 04. 03. 2011 12:47
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
↑ Tomaskocz:
Však ti taky nikdo neradil, abys derivoval S^2.
Offline
#33 04. 03. 2011 17:12
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
↑ Tomaskocz:, ↑ Tomaskocz: děkuji za hlášení.
↑ Honzc:
kolega Olin doporučoval na 1. str. tématu. Také v tomto tématu a zde se doporučovalo (děkuji autorům).
Také jsem to dřív nepoužívala, ale věřím doporučení a šířím dál.
Zdravím.
Offline
#34 04. 03. 2011 22:42
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
Tomaskocz napsal(a):
Takže příklad jsem obhájil, a odezva od učitele byla, že to není až tak zcela správné derivovat S^2 samozřejmě, že v našem případě to výjde správně, ale lepší by bylo derivovat S a né S^2 :-)
Pokud člověk dokáže zdůvodnit, proč to "v našem případě vyjde správně", je to správná metoda :-) Je škoda, když kantor ve svých žácích ubíjí kreativitu :-)
Offline
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Sestrojit trojuhelník v kružnici, aby měl co největší obsah (TOTO TÉMA JE VYŘEŠENÉ)
