Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Rovnice s neznámou v exponentu (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 03. 2011 13:58
Rovnice s neznámou v exponentu
Dobrý den, v předmětu mechanika jsme dostali zadání příkladu, se kterým si nedovedu poradit.
Můj problém spočívá ve vyjádření neznámě "x" z rovnice:
2000*pi = 200*e^(-0.1x) + 20x - 200
Věřím, že pro někoho z Vás to bude jistě jednoduché, ale já bohužel vážně netušim jak na to, proto bych chtěl poprosit o radu, ale potřeboval vych to i s postupem.
Děkuju Vám moc předem. Mějte se.
Offline
- (téma jako vyřešené označil(a) jelena)
#2 17. 03. 2011 14:46
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rovnice s neznámou v exponentu
Zdravím,
jsi si jistý, že potřebuješ vyjadřovat x? Není třeba řešení této rovnice pomocí některé z numerických metod?
až na podělení 20 levé a pravé strany rovnice další úpravy nepovědou k vyjádření běžnému na technické VŠ:
100*pi = 10*e^(-0.1x) + x - 10
potom úpravou na 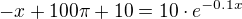 můžeš se pokusit najit řešení graficky (průsečík přímky a exponenciální funkce) nebo numerickou metodou.
můžeš se pokusit najit řešení graficky (průsečík přímky a exponenciální funkce) nebo numerickou metodou.
Můžeš svou rovnici zadat do Wolfram.
Jaké jiné úlohy tohoto typu jste řešili? Děkuji.
Offline
#3 17. 03. 2011 19:00
Re: Rovnice s neznámou v exponentu
Spíš já bych měl poděkovat, za odpověď nebo alespoň reakci :)
Příklad byl zadaný takto:
Doufám, že sem to vložil správně. Nicméně nejdřív sem si vyjádřil úhlovou rychlost jako integrál ze zrychlení podle t, pak úhlovou dráhu jako integrál z úhlové rychlosti podle t.
Pak sem si dal dráhu rovnou 2000*pi což odpovídá těm zadaným 1000 otáčkám, no a pak už sem nevěděl jak dál :) Jiné příklady s podobně, pro mě složitými rovnicemi jsme neměli, učiteli jde nejspíš o to abychom uměli používat ty integráli, bohužel já narazil trošku jinde než u nich. Mějte se.
Offline
#4 17. 03. 2011 19:17 — Editoval jelena (17. 03. 2011 21:57)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rovnice s neznámou v exponentu
Děkuji, zřejmě kolega to tady měl(a) také..
Popisuješ to dobře, ale napíš, prosím, jak jsi dointegroval k  , takový výsledek nebude, používáš substituci napr.
, takový výsledek nebude, používáš substituci napr.  , potom by neměl být problém výpočtu (snad).
, potom by neměl být problém výpočtu (snad).
Zkontroluj si integral nebo to sem napíš ke kontrole.
EDIT: zkontrolovala jsem integrování, zdá se, že máš v pořádku, potom jen numerické řešení, případně výsledek ve wolfram.
Offline
#6 17. 03. 2011 22:14
#7 18. 03. 2011 06:34 — Editoval Honzc (18. 03. 2011 06:36)
Re: Rovnice s neznámou v exponentu
↑ jelena:
Dle mého názoru, pro tento konkrétní případ, lze uvažovat takto:
Řešíme rovnici 10*(10*pi+1)-t=10/exp(0.1*t) pro t>0
Pokud položíme pravou stranu rovnice rovnu 0 dostaneme t=324.159265
Nyní dosadíme-li pro zkoušku do pravé strany toto t a dostaneme přibližně 8*10^(-14) což je číslo tak blízké nule, že pro náš fyzikální případ jej za 0 můžeme považovat.
Tedy stačilo vyřešit rovnici 10*(10*pi+1)-t=0
Po editaci.
Jinak daná rovnice lze řešit pouze numerickými metodami.
Offline
#8 18. 03. 2011 07:35
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rovnice s neznámou v exponentu
↑ Honzc:
Děkuji a zdravím.
kolega Honzc napsal(a):
Po editaci.
Jinak daná rovnice lze řešit pouze numerickými metodami.
Tomu bych věřila více, děkuji.
Offline
#9 18. 03. 2011 09:31
Re: Rovnice s neznámou v exponentu
↑ jelena:
"Přesné" řešení: Zde
Moje "přibližné" řešení: 324.159 26535 89793 23846 26433 83279 50288....
Což je jak je vidět rozdíl přibližně 0.8 pikosekundy.
Někde jsem četl, že poslední zemětřesení v Japonsku zkrátilo den o 1.8 mikrosekundy, což řádově milionkrát více než rozdíl v přesném a přibližném řešení této úlohy.
Pozn. Já jsem fakt, že se zkrátil den opravdu nezaznamenal.
Offline
#10 18. 03. 2011 11:05
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rovnice s neznámou v exponentu
↑ Honzc:
Děkuji.
Jelena včera napsal(a):
potom úpravou na
můžeš se pokusit najit řešení graficky (průsečík přímky a exponenciální funkce) nebo numerickou metodou.
Můžeš svou rovnici zadat do Wolfram.
Přibližné řešení vyplývá z předpokladu o chování exponenciální funkce tohoto zadání - je tak? U mne by vychozím krokem bylo grafické znázornění situace. A to mi bylo zakázano, dokonce opakovaně.
Pokud bych byla vystavena požadavku rovnici vyřešit bez použití strojů, tak bych grafickou situaci znázornila, co by mi zbyvalo.
Ovšem:
kolega Honzc napsal(a):
Pokud položíme pravou stranu rovnice rovnu 0 dostaneme t=324.159265
A tady mi chyběl předpoklad, z čeho jsi vycházel při položení pravé strany 0. Proto má reakce, ale jinak vím, že nemám psát před poledném.
Měj se hezky.
Offline
#12 20. 03. 2011 10:08
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Rovnice s neznámou v exponentu (TOTO TÉMA JE VYŘEŠENÉ)

