Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita složené funkce (TOTO TÉMA JE VYŘEŠENÉ)
#1 05. 04. 2011 20:06
Limita složené funkce
Ahoj, s timhle si nevim rady:
Jak na složenou funkci vím, ale nedokážu se poprat s tím vnitřkem závorky. V obou logaritmech mi vznikne jak v čitateli, tak i ve jmenovateli něco limitně se blížící 2, což neumím upravit. Nedokážu z těch exponentů dostat x, abych ho vykrátil.
Můžete mě někdo kopnout, ať mě napadne řešení?
Díky
Offline
- (téma jako vyřešené označil(a) mancini)
#2 05. 04. 2011 20:59
Re: Limita složené funkce
Snad to bude jasné a k přečtení
http://www.sdilej.eu/pics/c85310c379fe7 … 108f5b.jpg
...a zkusil si použít trojčlenku? :)
Offline
#3 05. 04. 2011 21:13
Re: Limita složené funkce
↑ Raduse73: diky moc ...
A existuje nejake elegantni reseni bez l'H?
Offline
#4 05. 04. 2011 21:37 — Editoval claudia (05. 04. 2011 21:59)
Re: Limita složené funkce
snad jsem se nikde nedopustila žádné ilegality... :-)
Offline
#5 05. 04. 2011 22:09 — Editoval OiBobik (05. 04. 2011 22:11)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Limita složené funkce
snad jsem se nikde nedopustila žádné ilegality... :-)
Jenom drobné, nepodstatné (píšu to jen proto, že náhodou jsem tu samou věc udělal na písemce o pololetí a zároveň se pokusil na toto reagovat, tak jsem to na tom chtěl vypíchnout):
Poznámka se týká úpravy následujícího: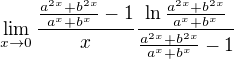
Použilo se věty o limitě složené funkce - verzi (P) (vnitřní funkce na nějakém okolí 0 nenabývá hodnoty své limity, tedy 0) můžeme předem zavrhnout, protože jinak bychom museli dlouze diskutovat, jaké ony parametry a, b musí být, aby  ... např. pro a=b=1 to zřejmě neplatí
... např. pro a=b=1 to zřejmě neplatí
Musíme tedy sáhnout po variantě (S)(vnější funkce v 0 spojitá) - ovšem to musíme uvážit ne funkci 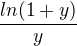 , nýbrž
, nýbrž
Tedy dodefinovat danou funkci v 0 její limitou. Ta už je i spojitá v bodě 0 a můžeme "legálně" použít VLSF(S). ; ))
Možná je to jenom nimrání se v detailech a možná si to všechno uvědomuješ, v tom případě se nezlob, ale přišlo mi zajímavé natolik, aby to alespoň stálo za zmínku.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#6 05. 04. 2011 22:31
Re: Limita složené funkce
↑ claudia:
jsem debil, ze jsem se snazil asi petkrat pracovat ruzne s citatelem a jmenovatelem zvlast, zkousel jsem vnitrek zavorky rozlozit na dva zlomky, ale nevim, proc me nenapadlo s tou hruzou v zavorce pracovat takhle :-(
diky moc
Offline
#7 05. 04. 2011 22:51 — Editoval claudia (05. 04. 2011 22:52)
Re: Limita složené funkce
↑ OiBobik:
Myslím, že je to velmi precizně osvětleno :-) (A velmi přesně jsi uhodl, kterou podmínku se mi nechtělo příliš podrobně ověřovat O:-)
↑ mancini:
Z toho si nic nedělej. To se stává každému.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita složené funkce (TOTO TÉMA JE VYŘEŠENÉ)
